| << Chapter < Page | Chapter >> Page > |
When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal stretch from a vertical stretch?
When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal compression from a vertical compression?
A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.
When examining the formula of a function that is the result of multiple transformations, how can you tell a reflection with respect to the x -axis from a reflection with respect to the y -axis?
How can you determine whether a function is odd or even from the formula of the function?
For a function substitute for in Simplify. If the resulting function is the same as the original function, then the function is even. If the resulting function is the opposite of the original function, then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.
For the following exercises, write a formula for the function obtained when the graph is shifted as described.
is shifted up 1 unit and to the left 2 units.
is shifted down 4 units and to the right 3 units.
For the following exercises, describe how the graph of the function is a transformation of the graph of the original function
The graph of is a horizontal shift to the left 43 units of the graph of
The graph of is a horizontal shift to the right 4 units of the graph of
The graph of is a vertical shift down 7 units of the graph of
The graph of is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of
For the following exercises, determine the interval(s) on which the function is increasing and decreasing.
For the following exercises, use the graph of shown in [link] to sketch a graph of each transformation of
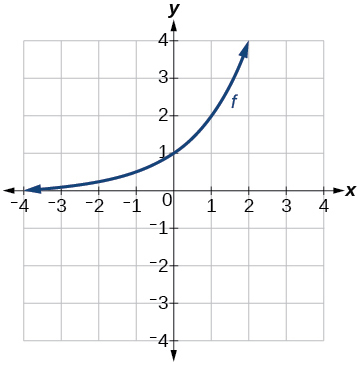
For the following exercises, sketch a graph of the function as a transformation of the graph of one of the toolkit functions.
Tabular representations for the functions and are given below. Write and as transformations of
| −2 | −1 | 0 | 1 | 2 | |
| −2 | −1 | −3 | 1 | 2 |
| −1 | 0 | 1 | 2 | 3 | |
| −2 | −1 | −3 | 1 | 2 |
| −2 | −1 | 0 | 1 | 2 | |
| −1 | 0 | −2 | 2 | 3 |
Tabular representations for the functions and are given below. Write and as transformations of
| −2 | −1 | 0 | 1 | 2 | |
| −1 | −3 | 4 | 2 | 1 |
| −3 | −2 | −1 | 0 | 1 | |
| −1 | −3 | 4 | 2 | 1 |
| −2 | −1 | 0 | 1 | 2 | |
| −2 | −4 | 3 | 1 | 0 |
For the following exercises, write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
For the following exercises, use the graphs of transformations of the square root function to find a formula for each of the functions.
For the following exercises, use the graphs of the transformed toolkit functions to write a formula for each of the resulting functions.
For the following exercises, determine whether the function is odd, even, or neither.
For the following exercises, describe how the graph of each function is a transformation of the graph of the original function
The graph of is a vertical reflection (across the -axis) of the graph of
The graph of is a vertical stretch by a factor of 4 of the graph of
The graph of is a horizontal compression by a factor of of the graph of
The graph of is a horizontal stretch by a factor of 3 of the graph of
The graph of is a horizontal reflection across the -axis and a vertical stretch by a factor of 3 of the graph of
For the following exercises, write a formula for the function that results when the graph of a given toolkit function is transformed as described.
The graph of is reflected over the - axis and horizontally compressed by a factor of .
The graph of is reflected over the -axis and horizontally stretched by a factor of 2.
The graph of is vertically compressed by a factor of then shifted to the left 2 units and down 3 units.
The graph of is vertically stretched by a factor of 8, then shifted to the right 4 units and up 2 units.
The graph of is vertically compressed by a factor of then shifted to the right 5 units and up 1 unit.
The graph of is horizontally stretched by a factor of 3, then shifted to the left 4 units and down 3 units.
For the following exercises, describe how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.
The graph of the function is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.
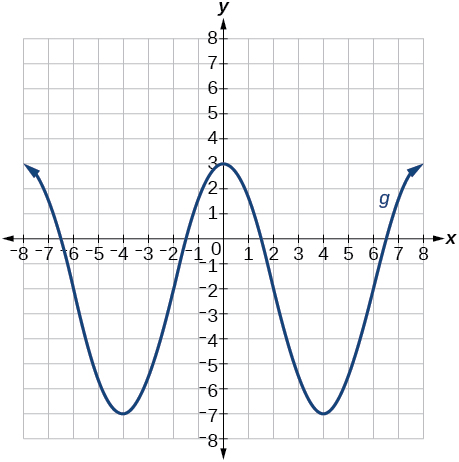
The graph of is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.
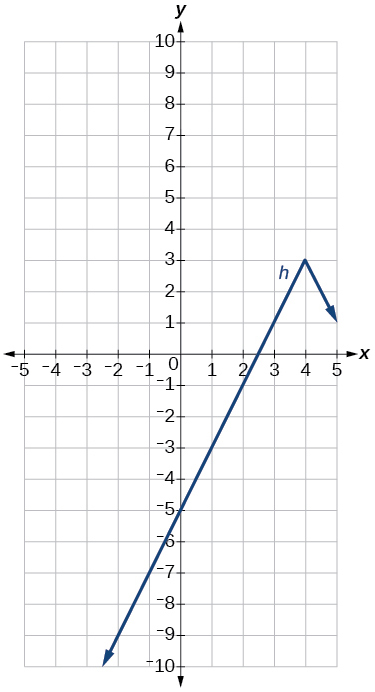
The graph of the function is compressed vertically by a factor of
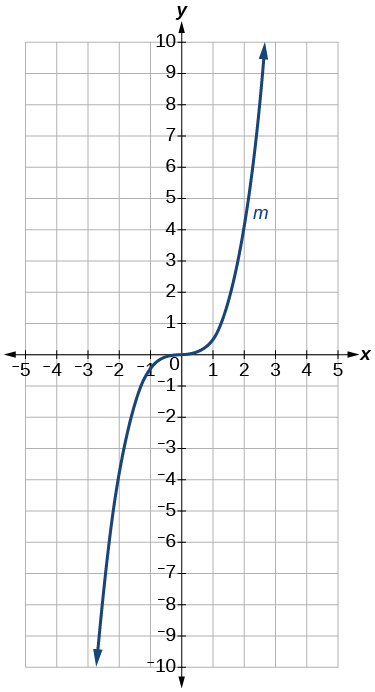
The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.
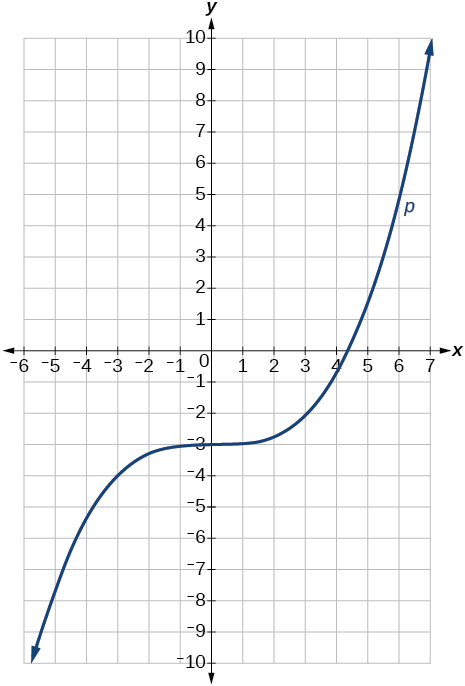
The graph of is shifted right 4 units and then reflected across the vertical line
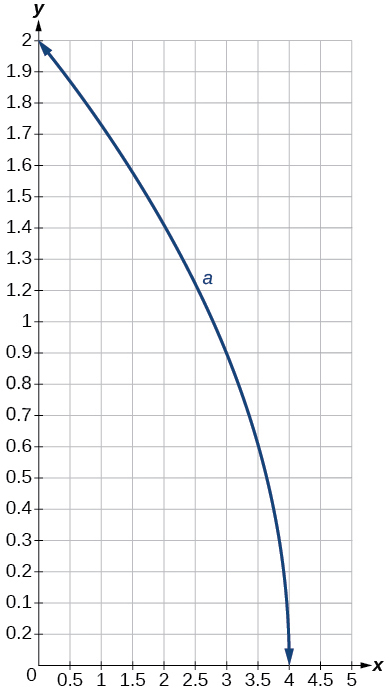
For the following exercises, use the graph in [link] to sketch the given transformations.
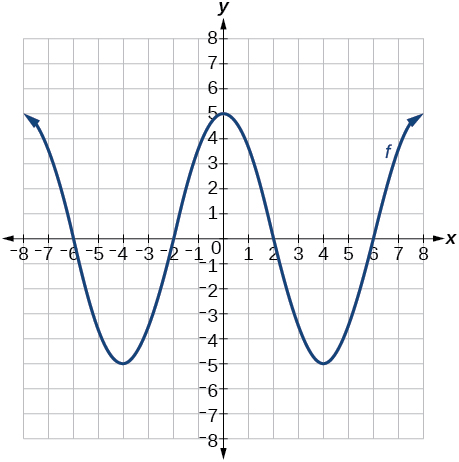

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?