| << Chapter < Page | Chapter >> Page > |
A solenoid with an iron core is 25 cm long and is wrapped with 100 turns of wire. When the current through the solenoid is 10 A, the magnetic field inside it is 2.0 T. For this current, what is the permeability of the iron? If the current is turned off and then restored to 10 A, will the magnetic field necessarily return to 2.0 T?
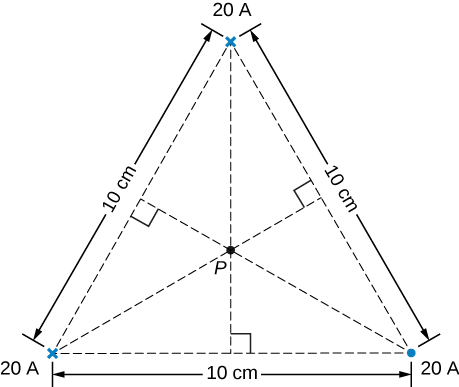
Three long, straight, parallel wires, all carrying 20 A, are positioned as shown in the accompanying figure. What is the magnitude of the magnetic field at the point P ?
A current I flows around a wire bent into the shape of a square of side a . What is the magnetic field at the point P that is a distance z above the center of the square (see the accompanying figure)?
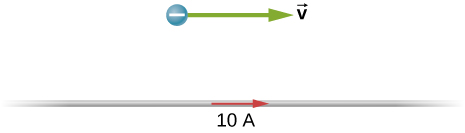
The accompanying figure shows a long, straight wire carrying a current of 10 A. What is the magnetic force on an electron at the instant it is 20 cm from the wire, traveling parallel to the wire with a speed of Describe qualitatively the subsequent motion of the electron.
in an arc away from the wire
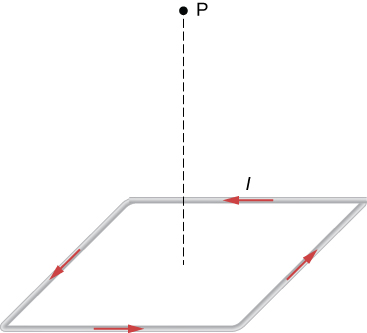
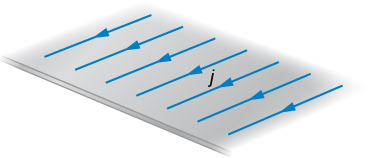
Current flows along a thin, infinite sheet as shown in the accompanying figure. The current per unit length along the sheet is J in amperes per meter. (a) Use the Biot-Savart law to show that on either side of the sheet. What is the direction of on each side? (b) Now use Ampère’s law to calculate the field.
(a) Use the result of the previous problem to calculate the magnetic field between, above, and below the pair of infinite sheets shown in the accompanying figure. (b) Repeat your calculations if the direction of the current in the lower sheet is reversed.
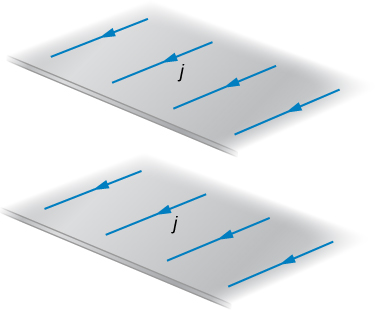
a. above and below in the middle b. above and below in the middle
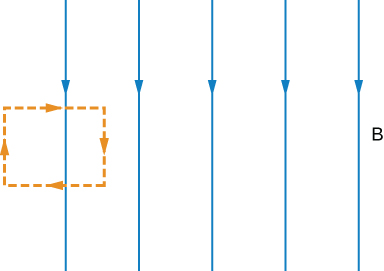
We often assume that the magnetic field is uniform in a region and zero everywhere else. Show that in reality it is impossible for a magnetic field to drop abruptly to zero, as illustrated in the accompanying figure. ( Hint : Apply Ampère’s law over the path shown.)
How is the percentage change in the strength of the magnetic field across the face of the toroid related to the percentage change in the radial distance from the axis of the toroid?
Show that the expression for the magnetic field of a toroid reduces to that for the field of an infinite solenoid in the limit that the central radius goes to infinity.
A toroid with an inner radius of 20 cm and an outer radius of 22 cm is tightly wound with one layer of wire that has a diameter of 0.25 mm. (a) How many turns are there on the toroid? (b) If the current through the toroid windings is 2.0 A, what is the strength of the magnetic field at the center of the toroid?
a. 52778 turns; b. 0.10 T
A wire element has
where
A and
dv are the cross-sectional area and volume of the element, respectively. Use this, the Biot-Savart law, and
to show that the magnetic field of a moving point charge q is given by:
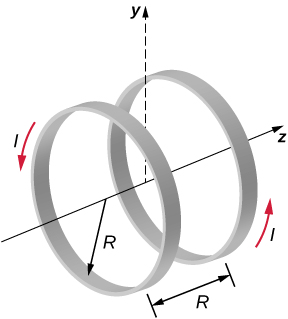
A reasonably uniform magnetic field over a limited region of space can be produced with the Helmholtz coil, which consists of two parallel coils centered on the same axis. The coils are connected so that they carry the same current I . Each coil has N turns and radius R , which is also the distance between the coils. (a) Find the magnetic field at any point on the z -axis shown in the accompanying figure. (b) Show that dB / dz and are both zero at z = 0. (These vanishing derivatives demonstrate that the magnetic field varies only slightly near z = 0.)

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?