2.4 Products of vectors (Page 8/16)

University physics volume 1 Page 8 / 16

Key equations

Multiplication by a scalar (vector equation)	$\vec{B} = α \vec{A}$
Multiplication by a scalar (scalar equation for magnitudes)	$B = \| α \| A$
Resultant of two vectors	${\vec{D}}_{A D} = {\vec{D}}_{A C} + {\vec{D}}_{C D}$
Commutative law	$\vec{A} + \vec{B} = \vec{B} + \vec{A}$
Associative law	$(\vec{A} + \vec{B}) + \vec{C} = \vec{A} + (\vec{B} + \vec{C})$
Distributive law	$α_{1} \vec{A} + α_{2} \vec{A} = (α_{1} + α_{2}) \vec{A}$
The component form of a vector in two dimensions	$\vec{A} = A_{x} \hat{i} + A_{y} \hat{j}$
Scalar components of a vector in two dimensions	${\begin{matrix} A_{x} = x_{e} - x_{b} \\ A_{y} = y_{e} - y_{b} \end{matrix}$
Magnitude of a vector in a plane	$A = \sqrt{A_{x}^{2} + A_{y}^{2}}$
The direction angle of a vector in a plane	$θ_{A} = {tan}^{−1} (\frac{A_{y}}{A_{x}})$
Scalar components of a vector in a plane	${\begin{matrix} A_{x} = A cos θ_{A} \\ A_{y} = A sin θ_{A} \end{matrix}$
Polar coordinates in a plane	${\begin{matrix} x = r cos φ \\ y = r sin φ \end{matrix}$
The component form of a vector in three dimensions	$\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k}$
The scalar z -component of a vector in three dimensions	$A_{z} = z_{e} - z_{b}$
Magnitude of a vector in three dimensions	$A = \sqrt{A_{x}^{2} + A_{y}^{2} + A_{z}^{2}}$
Distributive property	$α (\vec{A} + \vec{B}) = α \vec{A} + α \vec{B}$
Antiparallel vector to $\vec{A}$	$− \vec{A} = − A_{x} \hat{i} - A_{y} \hat{j} - A_{z} \hat{k}$
Equal vectors	$\vec{A} = \vec{B} \Leftrightarrow {\begin{matrix} A_{x} = B_{x} \\ A_{y} = B_{y} \\ A_{z} = B_{z} \end{matrix}$
Components of the resultant of N vectors	${\begin{matrix} F_{R x} = \sum_{k = 1}^{N} F_{k x} = F_{1 x} + F_{2 x} + … + F_{N x} \\ F_{R y} = \sum_{k = 1}^{N} F_{k y} = F_{1 y} + F_{2 y} + … + F_{N y} \\ F_{R z} = \sum_{k = 1}^{N} F_{k z} = F_{1 z} + F_{2 z} + … + F_{N z} \end{matrix}$
General unit vector	$\hat{V} = \frac{\vec{V}}{V}$
Definition of the scalar product	$\vec{A} \cdot \vec{B} = A B cos φ$
Commutative property of the scalar product	$\vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{A}$
Distributive property of the scalar product	$\vec{A} \cdot (\vec{B} + \vec{C}) = \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C}$
Scalar product in terms of scalar components of vectors	$\vec{A} \cdot \vec{B} = A_{x} B_{x} + A_{y} B_{y} + A_{z} B_{z}$
Cosine of the angle between two vectors	$cos φ = \frac{\vec{A} \cdot \vec{B}}{A B}$
Dot products of unit vectors	$\hat{i} \cdot \hat{j} = \hat{j} \cdot \hat{k} = \hat{k} \cdot \hat{i} = 0$
Magnitude of the vector product (definition)	$\| \vec{A} \times \vec{B} \| = A B sin φ$
Anticommutative property of the vector product	$\vec{A} \times \vec{B} = − \vec{B} \times \vec{A}$
Distributive property of the vector product	$\vec{A} \times (\vec{B} + \vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C}$
Cross products of unit vectors	${\begin{cases} \hat{i} \times \hat{j} = + \hat{k}, \\ \hat{j} \times \hat{k} = + \hat{i}, \\ \hat{k} \times \hat{i} = + \hat{j} . \end{cases}$
The cross product in terms of scalar components of vectors	$\vec{A} \times \vec{B} = (A_{y} B_{z} - A_{z} B_{y}) \hat{i} + (A_{z} B_{x} - A_{x} B_{z}) \hat{j} + (A_{x} B_{y} - A_{y} B_{x}) \hat{k}$

Conceptual questions

What is wrong with the following expressions? How can you correct them? (a) $C = \vec{A} \vec{B}$ , (b) $\vec{C} = \vec{A} \vec{B}$ , (c) $C = \vec{A} \times \vec{B}$ , (d) $C = A \vec{B}$ , (e) $C + 2 \vec{A} = B$ , (f) $\vec{C} = A \times \vec{B}$ , (g) $\vec{A} \cdot \vec{B} = \vec{A} \times \vec{B}$ , (h) $\vec{C} = 2 \vec{A} \cdot \vec{B}$ , (i) $C = \vec{A} / \vec{B}$ , and (j) $C = \vec{A} / B$ .

a. $C = \vec{A} \cdot \vec{B}$ , b. $\vec{C} = \vec{A} \times \vec{B}$ or $\vec{C} = \vec{A} - \vec{B}$ , c. $\vec{C} = \vec{A} \times \vec{B}$ , d. $\vec{C} = A \vec{B}$ , e. $\vec{C} + 2 \vec{A} = \vec{B}$ , f. $\vec{C} = \vec{A} \times \vec{B}$ , g. left side is a scalar and right side is a vector, h. $\vec{C} = 2 \vec{A} \times \vec{B}$ , i. $\vec{C} = \vec{A} / B$ , j. $\vec{C} = \vec{A} / B$

Got questions? Get instant answers now!

If the cross product of two vectors vanishes, what can you say about their directions?

Got questions? Get instant answers now!

If the dot product of two vectors vanishes, what can you say about their directions?

They are orthogonal.

Got questions? Get instant answers now!

What is the dot product of a vector with the cross product that this vector has with another vector?

Got questions? Get instant answers now!

Problems

Assuming the + x -axis is horizontal to the right for the vectors in the following figure, find the following scalar products: (a) $\vec{A} \cdot \vec{C}$ , (b) $\vec{A} \cdot \vec{F}$ , (c) $\vec{D} \cdot \vec{C}$ , (d) $\vec{A} \cdot (\vec{F} + 2 \vec{C})$ , (e) $\hat{i} \cdot \vec{B}$ , (f) $\hat{j} \cdot \vec{B}$ , (g) $(3 \hat{i} - \hat{j}) \cdot \vec{B}$ , and (h) $\hat{B} \cdot \vec{B}$ .

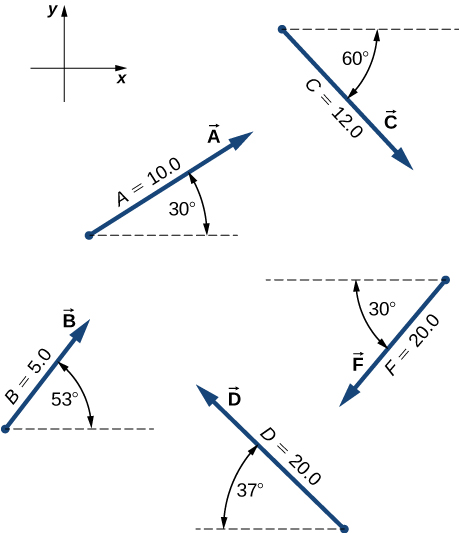
The x y coordinate system has positive x to the right and positive y up. Vector A has magnitude 10.0 and points 30 degrees counterclockwise from the positive x direction. Vector B has magnitude 5.0 and points 53 degrees counterclockwise from the positive x direction. Vector C has magnitude 12.0 and points 60 degrees clockwise from the positive x direction. Vector D has magnitude 20.0 and points 37 degrees clockwise from the negative x direction. Vector F has magnitude 20.0 and points 30 degrees counterclockwise from the negative x direction.

Got questions? Get instant answers now!

Assuming the + x -axis is horizontal to the right for the vectors in the preceding figure, find (a) the component of vector $\vec{A}$ along vector $\vec{C}$ , (b) the component of vector $\vec{C}$ along vector $\vec{A}$ , (c) the component of vector $\hat{i}$ along vector $\vec{F}$ , and (d) the component of vector $\vec{F}$ along vector $\hat{i}$ .

a. 8.66, b. 10.39, c. 0.866, d. 17.32

Got questions? Get instant answers now!

Find the angle between vectors for (a) $\vec{D} = (−3.0 \hat{i} - 4.0 \hat{j}) m$ and $\vec{A} = (−3.0 \hat{i} + 4.0 \hat{j}) m$ and (b) $\vec{D} = (2.0 \hat{i} - 4.0 \hat{j} + \hat{k}) m$ and $\vec{B} = (−2.0 \hat{i} + 3.0 \hat{j} + 2.0 \hat{k}) m$ .

Got questions? Get instant answers now!

Questions & Answers

prostaglandin and fever

Maha Reply

Discuss the differences between taste and flavor, including how other sensory inputs contribute to our perception of flavor.

John Reply

taste refers to your understanding of the flavor . while flavor one The other hand is refers to sort of just a blend things.

Faith

While taste primarily relies on our taste buds, flavor involves a complex interplay between taste and aroma

Kamara

which drugs can we use for ulcers

Ummi Reply

omeprazole

Kamara

what

Renee

what is this

Renee

is a drug

Kamara

of anti-ulcer

Kamara

Omeprazole Cimetidine / Tagament For the complicated once ulcer - kit

Patrick

what is the function of lymphatic system

Nency Reply

Not really sure

Eli

to drain extracellular fluid all over the body.

asegid

The lymphatic system plays several crucial roles in the human body, functioning as a key component of the immune system and contributing to the maintenance of fluid balance. Its main functions include: 1. Immune Response: The lymphatic system produces and transports lymphocytes, which are a type of

asegid

to transport fluids fats proteins and lymphocytes to the blood stream as lymph

Adama

what is anatomy

Oyindarmola Reply

Anatomy is the identification and description of the structures of living things

Kamara

what's the difference between anatomy and physiology

Oyerinde Reply

Anatomy is the study of the structure of the body, while physiology is the study of the function of the body. Anatomy looks at the body's organs and systems, while physiology looks at how those organs and systems work together to keep the body functioning.

AI-Robot

what is enzymes all about?

Mohammed Reply

Enzymes are proteins that help speed up chemical reactions in our bodies. Enzymes are essential for digestion, liver function and much more. Too much or too little of a certain enzyme can cause health problems

Kamara

yes

Prince

how does the stomach protect itself from the damaging effects of HCl

Wulku Reply

little girl okay how does the stomach protect itself from the damaging effect of HCL

Wulku

it is because of the enzyme that the stomach produce that help the stomach from the damaging effect of HCL

Kamara

function of digestive system

Ali Reply

function of digestive

Ali

the diagram of the lungs

Adaeze Reply

what is the normal body temperature

Diya Reply

37 degrees selcius

Xolo

37°c

Stephanie

please why 37 degree selcius normal temperature

Mark

36.5

Simon

37°c

Iyogho

the normal temperature is 37°c or 98.6 °Fahrenheit is important for maintaining the homeostasis in the body the body regular this temperature through the process called thermoregulation which involves brain skin muscle and other organ working together to maintain stable internal temperature

Stephanie

37A c

Wulku

what is anaemia

Diya Reply

anaemia is the decrease in RBC count hemoglobin count and PVC count

Eniola

what is the pH of the vagina

Diya Reply

how does Lysin attack pathogens

Diya

acid

Mary

I information on anatomy position and digestive system and there enzyme

Elisha Reply

anatomy of the female external genitalia

Muhammad Reply

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask

	2 AP Key Terms 02 Chemical Level of Organization By OpenStax Start Key Terms
©flickr: Steve	C Programming Language By JavaChamp Team Start Quiz
	23 Biology 23 Protists MCQ By OpenStax Start Quiz
	Unit 1 Geography Test By Qqq Qqq Start Flashcards
	7 Arts Society: Theater 7 By Jonathan Long Start Quiz
	Socialism Command Economy By Robert Murphy Start Test
	NCE Ch 09 Research and Program Evaluation By Anh Dao Start Quiz
	6 Microbiology Midterm Practice By Madison Christian Start Test
	20 Biology 20 Phylogenies the History of Life MCQ By OpenStax Start Quiz
	How to Analyze Stocks By Yasser Ibrahim Start Quiz