2.1 Scalars and vectors (Page 3/29)

University physics volume 1 Page 3 / 29

Two vectors that have identical directions are said to be parallel vectors —meaning, they are parallel to each other. Two parallel vectors $\vec{A}$ and $\vec{B}$ are equal, denoted by $\vec{A} = \vec{B}$ , if and only if they have equal magnitudes $| \vec{A} | = | \vec{B} |$ . Two vectors with directions perpendicular to each other are said to be orthogonal vectors . These relations between vectors are illustrated in [link] .

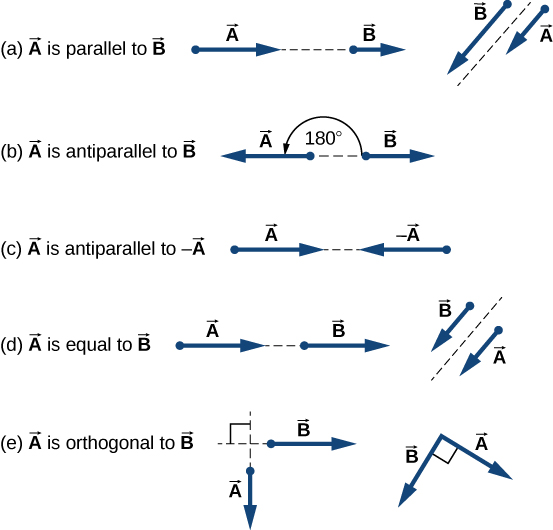
Figure a: Two examples of vector A parallel to vector B. In one, A and B are on the same line, one after the other, but A is longer than B. In the other, A and B are parallel to each other with their tails aligned, but A is shorter than B. Figure b: An example of vector A antiparallel to vector B. Vector A points to the left and is longer than vector B, which points to the right. The angle between them is 180 degrees. Figure c: An example of vector A antiparallel to minus vector A: A points to the right and –A points to the left. Both are the same length. Figure d: Two examples of vector A equal to vector B: In one, A and B are on the same line, one after the other, and both are the same length. In the other, A and B are parallel to each other with their tails aligned, and both are the same length. Figure e: Two examples of vector A orthogonal to vector B: In one, A points down and B points to the right, meeting at a right angle, and both are the same length. In the other, points down and to the right and B points down and to the left, meeting A at a right angle. Both are the same length. — Various relations between two vectors $\vec{A}$ and $\vec{B}$ . (a) $\vec{A} \neq \vec{B}$ because $A \neq B$ . (b) $\vec{A} \neq \vec{B}$ because they are not parallel and $A \neq B$ . (c) $\vec{A} \neq − \vec{A}$ because they have different directions (even though $| \vec{A} | = | - \vec{A} | = A)$ . (d) $\vec{A} = \vec{B}$ because they are parallel *and* have identical magnitudes A = B. (e) $\vec{A} \neq \vec{B}$ because they have different directions (are not parallel); here, their directions differ by $90 °$ —meaning, they are orthogonal.

Check Your Understanding Two motorboats named Alice and Bob are moving on a lake. Given the information about their velocity vectors in each of the following situations, indicate whether their velocity vectors are equal or otherwise. (a) Alice moves north at 6 knots and Bob moves west at 6 knots. (b) Alice moves west at 6 knots and Bob moves west at 3 knots. (c) Alice moves northeast at 6 knots and Bob moves south at 3 knots. (d) Alice moves northeast at 6 knots and Bob moves southwest at 6 knots. (e) Alice moves northeast at 2 knots and Bob moves closer to the shore northeast at 2 knots.

a. not equal because they are orthogonal; b. not equal because they have different magnitudes; c. not equal because they have different magnitudes and directions; d. not equal because they are antiparallel; e. equal.

Got questions? Get instant answers now!

Algebra of vectors in one dimension

Vectors can be multiplied by scalars, added to other vectors, or subtracted from other vectors. We can illustrate these vector concepts using an example of the fishing trip seen in [link] .

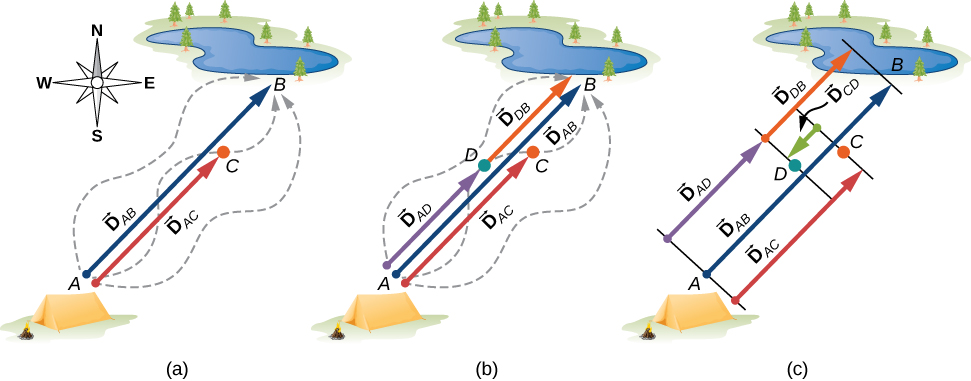
Three illustrations of the same tent and lake northeast of the tent. North is up on the page. The tent location is point A, and the lake location is point B. A location between A and B, about 2/3 of the way from A to B, is labeled as point C. In figure a, the vector from A to B is shown as a blue arrow, starting at A and ending at B, and labeled vector D sub A B. The vector from A to C is shown as a red arrow, starting at A and ending at C and labeled vector D sub A C. Three meandering paths are shown as dashed lines that start at A and end at B. Figure b adds the following to the illustration of figure a: Point D is added about half way between point A and B. The vector from A to D is shown as a purple arrow, starting at A and ending at D and labeled vector D sub A D. The vector from D to B is shown as an orange arrow, starting at D and ending at B and labeled vector D sub D B. Figure c adds a green arrow from point C to point D and is labeled vector D sub C D. Vector D sub C D points in the direction opposite to that of the other vectors, toward the tent rather than toward the lake. — Displacement vectors for a fishing trip. (a) Stopping to rest at point C while walking from camp (point A ) to the pond (point B ). (b) Going back for the dropped tackle box (point D ). (c) Finishing up at the fishing pond.

Suppose your friend departs from point A (the campsite) and walks in the direction to point B (the fishing pond), but, along the way, stops to rest at some point C located three-quarters of the distance between A and B , beginning from point A ( [link] (a)). What is his displacement vector ${\vec{D}}_{A C}$ when he reaches point C ? We know that if he walks all the way to B , his displacement vector relative to A is ${\vec{D}}_{A B}$ , which has magnitude $D_{A B} = 6 km$ and a direction of northeast. If he walks only a 0.75 fraction of the total distance, maintaining the northeasterly direction, at point C he must be $0.75 D_{A B} = 4.5 km$ away from the campsite at A . So, his displacement vector at the rest point C has magnitude $D_{A C} = 4.5 km = 0.75 D_{A B}$ and is parallel to the displacement vector ${\vec{D}}_{A B}$ . All of this can be stated succinctly in the form of the following vector equation :

{\vec{D}}_{A C} = 0.75 {\vec{D}}_{A B} .

In a vector equation, both sides of the equation are vectors. The previous equation is an example of a vector multiplied by a positive scalar (number) $α = 0.75$ . The result, ${\vec{D}}_{A C}$ , of such a multiplication is a new vector with a direction parallel to the direction of the original vector ${\vec{D}}_{A B}$ .

<< Chapter < Page Page > Chapter >>

Practice Key Terms 20

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask

	Grade 10 Module 2.1 IT Quiz (Part 1) By Christine Zeelie Start Quiz
	13 Sociology 13 Aging and the Elderly MCQ By OpenStax Start Quiz
	Social Psychology MCQ By Saylor Foundation Start Quiz
	12 Sociology 12 Gender, Sex, and Sexuality MCQ By OpenStax Start Quiz
©flickr:	Spanish Test By Tess Armstrong Start Quiz
©flickr: Mike	Examples of Wiffle IQ By Sean WiffleBoy Start Quiz
	Anthropology Religion Culture By Richley Crapo Start Assignment
	Elementary algebra By OpenStax Read Online Course
©flickr: Abraham	Multicellular Organisms Test By Monty Hartfield Start Test
	Statistics Final Review By Madison Christian Start Exam