| << Chapter < Page | Chapter >> Page > |
In 1653, the French philosopher and scientist Blaise Pascal published his Treatise on the Equilibrium of Liquids , in which he discussed principles of static fluids. A static fluid is a fluid that is not in motion. When a fluid is not flowing, we say that the fluid is in static equilibrium. If the fluid is water, we say it is in hydrostatic equilibrium . For a fluid in static equilibrium, the net force on any part of the fluid must be zero; otherwise the fluid will start to flow.
Pascal’s observations—since proven experimentally—provide the foundation for hydraulics , one of the most important developments in modern mechanical technology. Pascal observed that a change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid and to the walls of its container. Because of this, we often know more about pressure than other physical quantities in fluids. Moreover, Pascal’s principle implies that the total pressure in a fluid is the sum of the pressures from different sources. A good example is the fluid at a depth depends on the depth of the fluid and the pressure of the atmosphere.
Pascal’s principle (also known as Pascal’s law) states that when a change in pressure is applied to an enclosed fluid, it is transmitted undiminished to all portions of the fluid and to the walls of its container. In an enclosed fluid, since atoms of the fluid are free to move about, they transmit pressure to all parts of the fluid and to the walls of the container. Any change in pressure is transmitted undiminished.
Note that this principle does not say that the pressure is the same at all points of a fluid—which is not true, since the pressure in a fluid near Earth varies with height. Rather, this principle applies to the change in pressure. Suppose you place some water in a cylindrical container of height H and cross-sectional area A that has a movable piston of mass m ( [link] ). Adding weight Mg at the top of the piston increases the pressure at the top by Mg / A , since the additional weight also acts over area A of the lid:
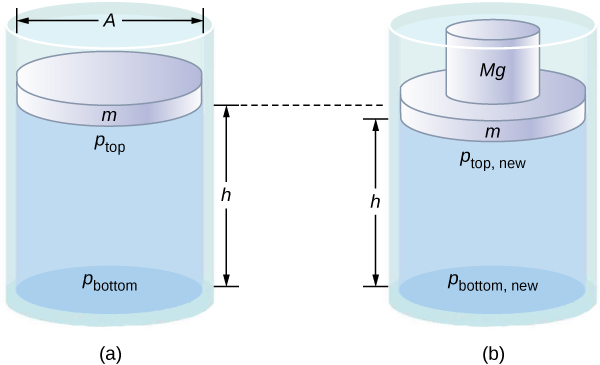
According to Pascal’s principle, the pressure at all points in the water changes by the same amount, Mg / A . Thus, the pressure at the bottom also increases by Mg / A . The pressure at the bottom of the container is equal to the sum of the atmospheric pressure, the pressure due the fluid, and the pressure supplied by the mass. The change in pressure at the bottom of the container due to the mass is
Since the pressure changes are the same everywhere in the fluid, we no longer need subscripts to designate the pressure change for top or bottom:

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?