| << Chapter < Page | Chapter >> Page > |
A weather forecast states the temperature is predicted to be the following day. Is this temperature a vector or a scalar quantity? Explain.
scalar
Which of the following is a vector: a person’s height, the altitude on Mt. Everest, the velocity of a fly, the age of Earth, the boiling point of water, the cost of a book, Earth’s population, or the acceleration of gravity?
Give a specific example of a vector, stating its magnitude, units, and direction.
answers may vary
What do vectors and scalars have in common? How do they differ?
Suppose you add two vectors and . What relative direction between them produces the resultant with the greatest magnitude? What is the maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?
parallel, sum of magnitudes, antiparallel, zero
Is it possible to add a scalar quantity to a vector quantity?
Is it possible for two vectors of different magnitudes to add to zero? Is it possible for three vectors of different magnitudes to add to zero? Explain.
no, yes
Does the odometer in an automobile indicate a scalar or a vector quantity?
When a 10,000-m runner competing on a 400-m track crosses the finish line, what is the runner’s net displacement? Can this displacement be zero? Explain.
zero, yes
A vector has zero magnitude. Is it necessary to specify its direction? Explain.
Can the magnitude of a particle’s displacement be greater that the distance traveled?
If two vectors are equal, what can you say about their components? What can you say about their magnitudes? What can you say about their directions?
equal, equal, the same
If three vectors sum up to zero, what geometric condition do they satisfy?
A scuba diver makes a slow descent into the depths of the ocean. His vertical position with respect to a boat on the surface changes several times. He makes the first stop 9.0 m from the boat but has a problem with equalizing the pressure, so he ascends 3.0 m and then continues descending for another 12.0 m to the second stop. From there, he ascends 4 m and then descends for 18.0 m, ascends again for 7 m and descends again for 24.0 m, where he makes a stop, waiting for his buddy. Assuming the positive direction up to the surface, express his net vertical displacement vector in terms of the unit vector. What is his distance to the boat?
, 49 m
In a tug-of-war game on one campus, 15 students pull on a rope at both ends in an effort to displace the central knot to one side or the other. Two students pull with force 196 N each to the right, four students pull with force 98 N each to the left, five students pull with force 62 N each to the left, three students pull with force 150 N each to the right, and one student pulls with force 250 N to the left. Assuming the positive direction to the right, express the net pull on the knot in terms of the unit vector. How big is the net pull on the knot? In what direction?
Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point and what is the compass direction of a line connecting your starting point to your final position? Use a graphical method.
30.8 m, west of north
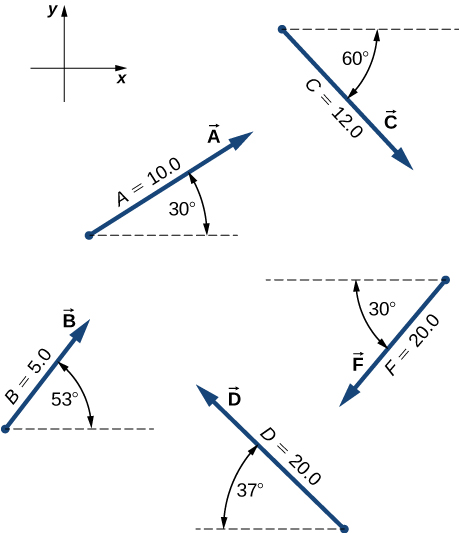
For the vectors given in the following figure, use a graphical method to find the following resultants: (a) , (b) , (c) , (d) , (e) , (f) , (g); and (h) .
A delivery man starts at the post office, drives 40 km north, then 20 km west, then 60 km northeast, and finally 50 km north to stop for lunch. Use a graphical method to find his net displacement vector.
134 km,
An adventurous dog strays from home, runs three blocks east, two blocks north, one block east, one block north, and two blocks west. Assuming that each block is about 100 m, how far from home and in what direction is the dog? Use a graphical method.
In an attempt to escape a desert island, a castaway builds a raft and sets out to sea. The wind shifts a great deal during the day and he is blown along the following directions: 2.50 km and north of west, then 4.70 km and south of east, then 1.30 km and south of west, then 5.10 km straight east, then 1.70 km and east of north, then 7.20 km and south of west, and finally 2.80 km and north of east. Use a graphical method to find the castaway’s final position relative to the island.
7.34 km, south of east
A small plane flies 40.0 km in a direction north of east and then flies 30.0 km in a direction north of east. Use a graphical method to find the total distance the plane covers from the starting point and the direction of the path to the final position.
A trapper walks a 5.0-km straight-line distance from his cabin to the lake, as shown in the following figure. Use a graphical method (the parallelogram rule) to determine the trapper’s displacement directly to the east and displacement directly to the north that sum up to his resultant displacement vector. If the trapper walked only in directions east and north, zigzagging his way to the lake, how many kilometers would he have to walk to get to the lake?
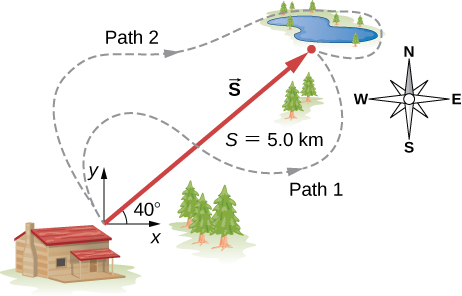
3.8 km east, 3.2 km north, 7.0 km
A surveyor measures the distance across a river that flows straight north by the following method. Starting directly across from a tree on the opposite bank, the surveyor walks 100 m along the river to establish a baseline. She then sights across to the tree and reads that the angle from the baseline to the tree is . How wide is the river?
A pedestrian walks 6.0 km east and then 13.0 km north. Use a graphical method to find the pedestrian’s resultant displacement and geographic direction.
14.3 km,
The magnitudes of two displacement vectors are A = 20 m and B = 6 m. What are the largest and the smallest values of the magnitude of the resultant

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?