| << Chapter < Page | Chapter >> Page > |
Two blocks connected by a string are pulled across a horizontal surface by a force applied to one of the blocks, as shown below. The coefficient of kinetic friction between the blocks and the surface is 0.25. If each block has an acceleration of to the right, what is the magnitude F of the applied force?
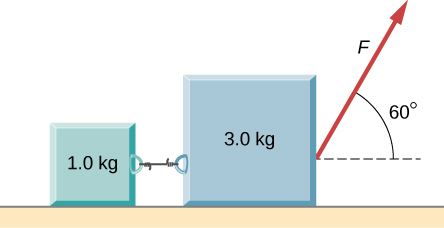
25 N
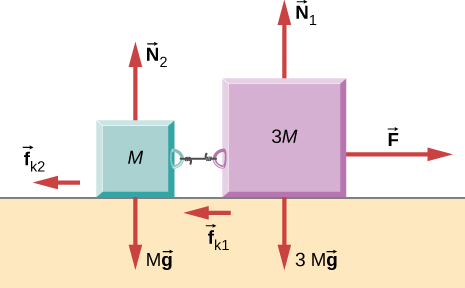
As shown below, the coefficient of kinetic friction between the surface and the larger block is 0.20, and the coefficient of kinetic friction between the surface and the smaller block is 0.30. If and , what is the tension in the connecting string?
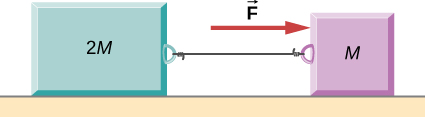
In the figure, the coefficient of kinetic friction between the surface and the blocks is If find an expression for the magnitude of the acceleration of either block (in terms of F , and g ).
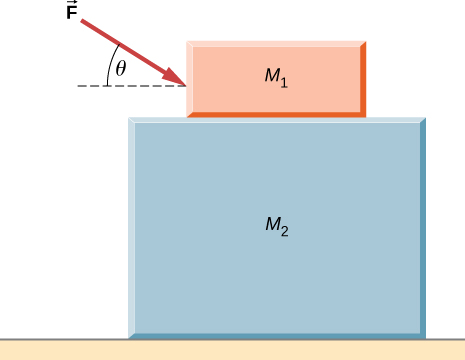
Two blocks are stacked as shown below, and rest on a frictionless surface. There is friction between the two blocks (coefficient of friction ). An external force is applied to the top block at an angle with the horizontal. What is the maximum force F that can be applied for the two blocks to move together?
A box rests on the (horizontal) back of a truck. The coefficient of static friction between the box and the surface on which it rests is 0.24. What maximum distance can the truck travel (starting from rest and moving horizontally with constant acceleration) in 3.0 s without having the box slide?
14 m
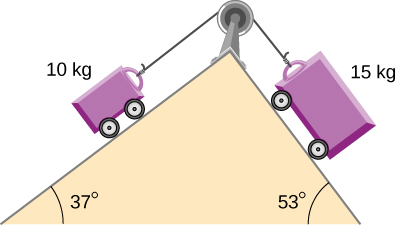
A double-incline plane is shown below. The coefficient of friction on the left surface is 0.30, and on the right surface 0.16. Calculate the acceleration of the system.
In a later chapter, you will find that the weight of a particle varies with altitude such that where is the radius of Earth and r is the distance from Earth’s center. If the particle is fired vertically with velocity from Earth’s surface, determine its velocity as a function of position r . ( Hint: use the rearrangement mentioned in the text.)
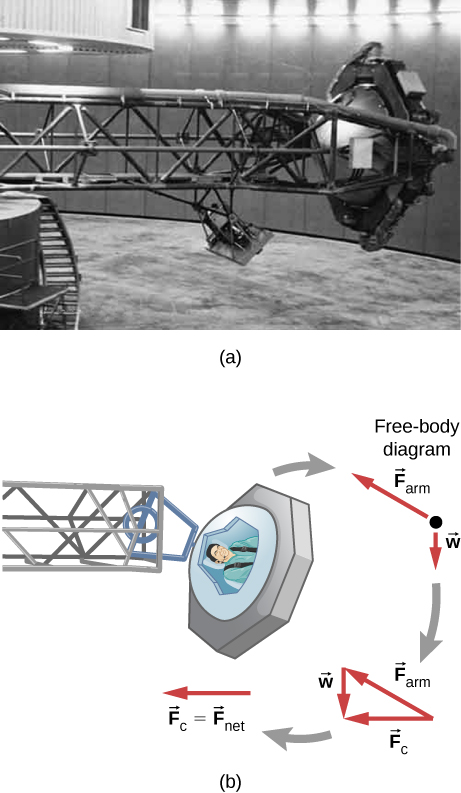
A large centrifuge, like the one shown below, is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric reentries. (a) At what angular velocity is the centripetal acceleration 10 g if the rider is 15.0 m from the center of rotation? (b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in the bottom accompanying figure. At what angle below the horizontal will the cage hang when the centripetal acceleration is 10 g ? ( Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free-body diagram of the forces to see what the angle should be.)
A car of mass 1000.0 kg is traveling along a level road at 100.0 km/h when its brakes are applied. Calculate the stopping distance if the coefficient of kinetic friction of the tires is 0.500. Neglect air resistance. ( Hint: since the distance traveled is of interest rather than the time, x is the desired independent variable and not t . Use the Chain Rule to change the variable:
78.7 m
An airplane flying at 200.0 m/s makes a turn that takes 4.0 min. What bank angle is required? What is the percentage increase in the perceived weight of the passengers?
A skydiver is at an altitude of 1520 m. After 10.0 seconds of free fall, he opens his parachute and finds that the air resistance, , is given by the formula where b is a constant and v is the velocity. If and the mass of the skydiver is 82.0 kg, first set up differential equations for the velocity and the position, and then find: (a) the speed of the skydiver when the parachute opens, (b) the distance fallen before the parachute opens, (c) the terminal velocity after the parachute opens (find the limiting velocity), and (d) the time the skydiver is in the air after the parachute opens.
a. 53.9 m/s; b. 328 m; c. 4.58 m/s; d. 257 s
In a television commercial, a small, spherical bead of mass 4.00 g is released from rest at in a bottle of liquid shampoo. The terminal speed is observed to be 2.00 cm/s. Find (a) the value of the constant b in the equation and (b) the value of the resistive force when the bead reaches terminal speed.
A boater and motor boat are at rest on a lake. Together, they have mass 200.0 kg. If the thrust of the motor is a constant force of 40.0 N in the direction of motion, and if the resistive force of the water is numerically equivalent to 2 times the speed v of the boat, set up and solve the differential equation to find: (a) the velocity of the boat at time t ; (b) the limiting velocity (the velocity after a long time has passed).
a. b.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?