| << Chapter < Page | Chapter >> Page > |
A car is moving at high speed along a highway when the driver makes an emergency braking. The wheels become locked (stop rolling), and the resulting skid marks are 32.0 meters long. If the coefficient of kinetic friction between tires and road is 0.550, and the acceleration was constant during braking, how fast was the car going when the wheels became locked?
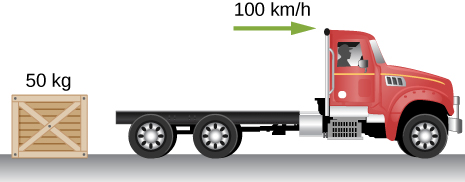
A crate having mass 50.0 kg falls horizontally off the back of the flatbed truck, which is traveling at 100 km/h. Find the value of the coefficient of kinetic friction between the road and crate if the crate slides 50 m on the road in coming to rest. The initial speed of the crate is the same as the truck, 100 km/h.
0.789
A 15-kg sled is pulled across a horizontal, snow-covered surface by a force applied to a rope at 30 degrees with the horizontal. The coefficient of kinetic friction between the sled and the snow is 0.20. (a) If the force is 33 N, what is the horizontal acceleration of the sled? (b) What must the force be in order to pull the sled at constant velocity?
A 30.0-g ball at the end of a string is swung in a vertical circle with a radius of 25.0 cm. The rotational velocity is 200.0 cm/s. Find the tension in the string: (a) at the top of the circle, (b) at the bottom of the circle, and (c) at a distance of 12.5 cm from the center of the circle
a. 0.186 N; b. 774 N; c. 0.48 N
A particle of mass 0.50 kg starts moves through a circular path in the xy -plane with a position given by where r is in meters and t is in seconds. (a) Find the velocity and acceleration vectors as functions of time. (b) Show that the acceleration vector always points toward the center of the circle (and thus represents centripetal acceleration). (c) Find the centripetal force vector as a function of time.
A stunt cyclist rides on the interior of a cylinder 12 m in radius. The coefficient of static friction between the tires and the wall is 0.68. Find the value of the minimum speed for the cyclist to perform the stunt.
13 m/s
When a body of mass 0.25 kg is attached to a vertical massless spring, it is extended 5.0 cm from its unstretched length of 4.0 cm. The body and spring are placed on a horizontal frictionless surface and rotated about the held end of the spring at 2.0 rev/s. How far is the spring stretched?
Railroad tracks follow a circular curve of radius 500.0 m and are banked at an angle of . For trains of what speed are these tracks designed?
20.7 m/s
A plumb bob hangs from the roof of a railroad car. The car rounds a circular track of radius 300.0 m at a speed of 90.0 km/h. At what angle relative to the vertical does the plumb bob hang?
An airplane flies at 120.0 m/s and banks at a angle. If its mass is (a) what is the magnitude of the lift force? (b) what is the radius of the turn?
a. 28,300 N; b. 2540 m
The position of a particle is given by where is a constant. (a) Show that the particle moves in a circle of radius A . (b) Calculate and then show that the speed of the particle is a constant (c) Determine and show that a is given by (d) Calculate the centripetal force on the particle. [ Hint : For (b) and (c), you will need to use and

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?