| << Chapter < Page | Chapter >> Page > |
A vector can be multiplied by another vector but may not be divided by another vector. There are two kinds of products of vectors used broadly in physics and engineering. One kind of multiplication is a scalar multiplication of two vectors . Taking a scalar product of two vectors results in a number (a scalar), as its name indicates. Scalar products are used to define work and energy relations. For example, the work that a force (a vector) performs on an object while causing its displacement (a vector) is defined as a scalar product of the force vector with the displacement vector. A quite different kind of multiplication is a vector multiplication of vectors . Taking a vector product of two vectors returns as a result a vector, as its name suggests. Vector products are used to define other derived vector quantities. For example, in describing rotations, a vector quantity called torque is defined as a vector product of an applied force (a vector) and its distance from pivot to force (a vector). It is important to distinguish between these two kinds of vector multiplications because the scalar product is a scalar quantity and a vector product is a vector quantity.
Scalar multiplication of two vectors yields a scalar product.
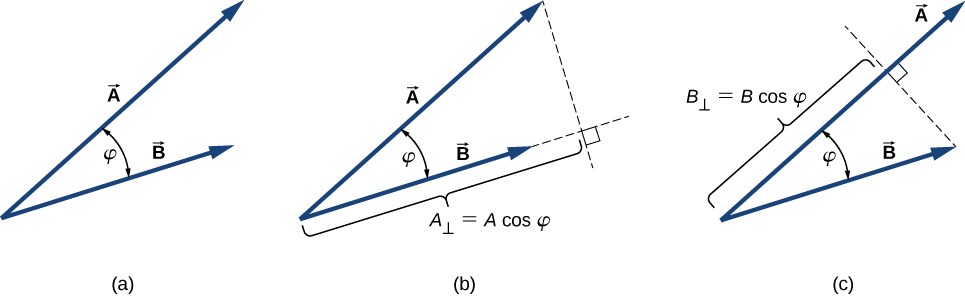
The scalar product of two vectors and is a number defined by the equation
where is the angle between the vectors (shown in [link] ). The scalar product is also called the dot product because of the dot notation that indicates it.
In the definition of the dot product, the direction of angle does not matter, and can be measured from either of the two vectors to the other because . The dot product is a negative number when and is a positive number when . Moreover, the dot product of two parallel vectors is , and the dot product of two antiparallel vectors is . The scalar product of two orthogonal vectors vanishes: . The scalar product of a vector with itself is the square of its magnitude:
Check Your Understanding For the vectors given in [link] , find the scalar products and .
,

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?