| << Chapter < Page | Chapter >> Page > |
In general, when a vector is multiplied by a positive scalar , the result is a new vector that is parallel to :
The magnitude of this new vector is obtained by multiplying the magnitude of the original vector, as expressed by the scalar equation :
In a scalar equation, both sides of the equation are numbers. [link] is a scalar equation because the magnitudes of vectors are scalar quantities (and positive numbers). If the scalar is negative in the vector equation [link] , then the magnitude of the new vector is still given by [link] , but the direction of the new vector is antiparallel to the direction of . These principles are illustrated in [link] (a) by two examples where the length of vector is 1.5 units. When , the new vector has length (twice as long as the original vector) and is parallel to the original vector. When , the new vector has length (twice as long as the original vector) and is antiparallel to the original vector.
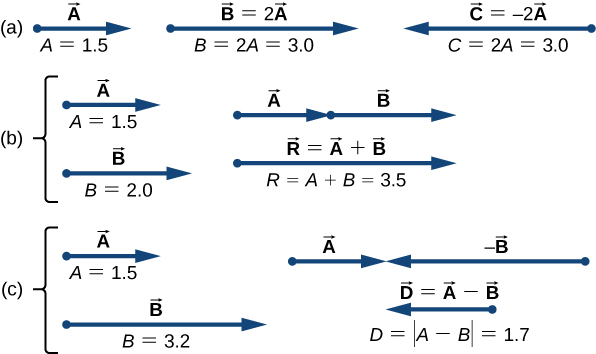
Now suppose your fishing buddy departs from point A (the campsite), walking in the direction to point B (the fishing hole), but he realizes he lost his tackle box when he stopped to rest at point C (located three-quarters of the distance between A and B , beginning from point A ). So, he turns back and retraces his steps in the direction toward the campsite and finds the box lying on the path at some point D only 1.2 km away from point C (see [link] (b)). What is his displacement vector when he finds the box at point D ? What is his displacement vector from point D to the hole? We have already established that at rest point C his displacement vector is . Starting at point C , he walks southwest (toward the campsite), which means his new displacement vector from point C to point D is antiparallel to . Its magnitude is , so his second displacement vector is . His total displacement relative to the campsite is the vector sum of the two displacement vectors: vector (from the campsite to the rest point) and vector (from the rest point to the point where he finds his box):
The vector sum of two (or more) vectors is called the resultant vector or, for short, the resultant . When the vectors on the right-hand-side of [link] are known, we can find the resultant as follows:
When your friend finally reaches the pond at B , his displacement vector from point A is the vector sum of his displacement vector from point A to point D and his displacement vector from point D to the fishing hole: (see [link] (c)). This means his displacement vector is the difference of two vectors :
Notice that a difference of two vectors is nothing more than a vector sum of two vectors because the second term in [link] is vector (which is antiparallel to . When we substitute [link] into [link] , we obtain the second displacement vector:

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?