| << Chapter < Page | Chapter >> Page > |
Suppose that the sound level from a source is 75 dB and then drops to 52 dB, with a frequency of 600 Hz. Determine the (a) initial and (b) final sound intensities and the (c) initial and (d) final sound wave amplitudes. The air temperature is and the air density is
; a. ; b. ; c. ; d.
The Doppler shift for a Doppler radar is found by , where is the frequency of the radar, f is the frequency observed by the radar, c is the speed of light, and v is the speed of the target. What is the beat frequency observed at the radar, assuming the speed of the target is much slower than the speed of light?
A stationary observer hears a frequency of 1000.00 Hz as a source approaches and a frequency of 850.00 Hz as a source departs. The source moves at a constant velocity of 75 mph. What is the temperature of the air?
A flute plays a note with a frequency of 600 Hz. The flute can be modeled as a pipe open at both ends, where the flute player changes the length with his finger positions. What is the length of the tube if this is the fundamental frequency?
Two sound speakers are separated by a distance d , each sounding a frequency f . An observer stands at one speaker and walks in a straight line a distance x , perpendicular to the the two speakers, until he comes to the first maximum intensity of sound. The speed of sound is v . How far is he from the speaker?
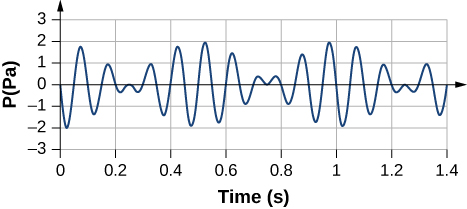
Consider the beats shown below. This is a graph of the gauge pressure versus time for the position The wave moves with a speed of (a) How many beats are there per second? (b) How many times does the wave oscillate per second? (c) Write a wave function for the gauge pressure as a function of time.
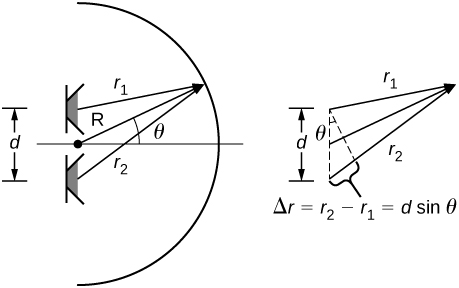
Two speakers producing the same frequency of sound are a distance of d apart. Consider an arc along a circle of radius R , centered at the midpoint of the speakers, as shown below. (a) At what angles will there be maxima? (b) At what angle will there be minima?
a. For maxima
b. For minima,
A string has a length of 1.5 m, a linear mass density , and a tension of 120 N. If the air temperature is what should the length of a pipe open at both ends for it to have the same frequency for the mode?
A string is fixed at both ends and is under a tension of 155 N. It oscillates in the mode and produces sound. A tuning fork is ringing nearby, producing a beat frequency of 23.76 Hz. (a) What is the frequency of the sound from the string? (b) What is the frequency of the tuning fork if the tuning fork frequency is lower? (c) What should be the tension of the string for the beat frequency to be zero?
a. ; b. ; c.
A string has a linear mass density , a length L , and a tension of , and oscillates in a mode n at a frequency f . Find the ratio of for a small change in tension.
A string has a linear mass density a length a tension of and oscillates in a mode . (a) What is the frequency of the oscillations? (b) Use the result in the preceding problem to find the change in the frequency when the tension is increased by .
a. ; b.
A speaker powered by a signal generator is used to study resonance in a tube. The signal generator can be adjusted from a frequency of 1000 Hz to 1800 Hz. First, a 0.75-m-long tube, open at both ends, is studied. The temperature in the room is (a) Which normal modes of the pipe can be studied? What are the frequencies and wavelengths? Next a cap is place on one end of the 0.75-meter-long pipe. (b) Which normal modes of the pipe can be studied? What are the frequencies and wavelengths?
A string on the violin has a length of 23.00 cm and a mass of 0.900 grams. The tension in the string 850.00 N. The temperature in the room is The string is plucked and oscillates in the mode. (a) What is the speed of the wave on the string? (b) What is the wavelength of the sounding wave produced? (c) What is the frequency of the oscillating string? (d) What is the frequency of the sound produced? (e) What is the wavelength of the sound produced?
a.
; b.
; c.
;
d.
; e.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?