-
Home
- University physics volume 1
- Unit 2. waves and acoustics
- Sound
- Shock waves
A speaker is placed at the opening of a long horizontal tube. The speaker oscillates at a frequency of
f , creating a sound wave that moves down the tube. The wave moves through the tube at a speed of
The sound wave is modeled with the wave function
. At time
, an air molecule at
is at the maximum displacement of 6.34 nm. At the same time, another molecule at
has a displacement of 2.30 nm. What is the wave function of the sound wave, that is, find the wave number, angular frequency, and the initial phase shift?
Got questions? Get instant answers now!
An airplane moves at Mach 1.2 and produces a shock wave. (a) What is the speed of the plane in meters per second? (b) What is the angle that the shock wave moves?
Got questions? Get instant answers now!
Additional problems
A 0.80-m-long tube is opened at both ends. The air temperature is
The air in the tube is oscillated using a speaker attached to a signal generator. What are the wavelengths and frequencies of first two modes of sound waves that resonate in the tube?
;
Got questions? Get instant answers now!
A tube filled with water has a valve at the bottom to allow the water to flow out of the tube. As the water is emptied from the tube, the length
L of the air column changes. A 1024-Hz tuning fork is placed at the opening of the tube. Water is removed from the tube until the
mode of a sound wave resonates. What is the length of the air column if the temperature of the air in the room is

Got questions? Get instant answers now!
Consider the following figure. The length of the string between the string vibrator and the pulley is
The linear density of the string is
The string vibrator can oscillate at any frequency. The hanging mass is 2.00 kg. (a)What are the wavelength and frequency of
mode? (b) The string oscillates the air around the string. What is the wavelength of the sound if the speed of the sound is
?
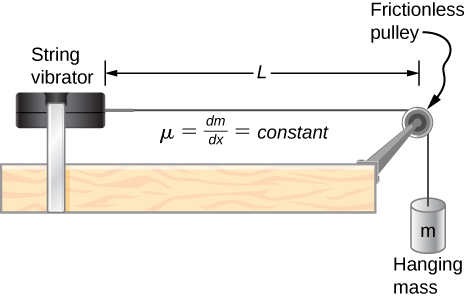
a.
; b.
Got questions? Get instant answers now!
Early Doppler shift experiments were conducted using a band playing music on a train. A trumpet player on a moving railroad flatcar plays a 320-Hz note. The sound waves heard by a stationary observer on a train platform hears a frequency of 350 Hz. What is the flatcar’s speed in mph? The temperature of the air is
.
Got questions? Get instant answers now!
Two cars move toward one another, both sounding their horns
. Car A is moving at 65 mph and Car B is at 75 mph. What is the beat frequency heard by each driver? The air temperature is
.
Got questions? Get instant answers now!
Student A runs after Student B. Student A carries a tuning fork ringing at 1024 Hz, and student B carries a tuning fork ringing at 1000 Hz. Student A is running at a speed of
and Student B is running at
What is the beat frequency heard by each student? The speed of sound is
Got questions? Get instant answers now!
Questions & Answers
what does preconceived mean
How can I develope my cognitive domain
why is communication effective
Communication is effective because it allows individuals to share ideas, thoughts, and information with others.
effective communication can lead to improved outcomes in various settings, including personal relationships, business environments, and educational settings. By communicating effectively, individuals can negotiate effectively, solve problems collaboratively, and work towards common goals.
it starts up serve and return practice/assessments.it helps find voice talking therapy also assessments through relaxed conversation.
miss
Every time someone flushes a toilet in the apartment building, the person begins to jumb back automatically after hearing the flush, before the water temperature changes. Identify the types of learning, if it is classical conditioning identify the NS, UCS, CS and CR. If it is operant conditioning, identify the type of consequence positive reinforcement, negative reinforcement or punishment
please i need answer
Wekolamo
because it helps many people around the world to understand how to interact with other people and understand them well, for example at work (job).
Agreed 👍 There are many parts of our brains and behaviors, we really need to get to know. Blessings for everyone and happy Sunday!
ARC
A child is a member of community not society elucidate ?
Isn't practices worldwide, be it psychology, be it science. isn't much just a false belief of control over something the mind cannot truly comprehend?
compare and contrast skinner's perspective on personality development on freud
Skinner skipped the whole unconscious phenomenon and rather emphasized on classical conditioning
war
explain how nature and nurture affect the development and later the productivity of an individual.
nature is an hereditary factor while nurture is an environmental factor which constitute an individual personality. so if an individual's parent has a deviant behavior and was also brought up in an deviant environment, observation of the behavior and the inborn trait we make the individual deviant.
Samuel
I am taking this course because I am hoping that I could somehow learn more about my chosen field of interest and due to the fact that being a PsyD really ignites my passion as an individual the more I hope to learn about developing and literally explore the complexity of my critical thinking skills
and having a good philosophy of the world is like a sandwich and a peanut butter 👍
Jonathan
generally amnesi how long yrs memory loss
interpersonal relationships
What would be the best educational aid(s) for gifted kids/savants?
treat them normal, if they want help then give them.
that will make everyone happy
Saurabh
What are the treatment for autism?
hello. autism is a umbrella term. autistic kids have different disorder overlapping. for example. a kid may show symptoms of ADHD and also learning disabilities.
before treatment please make sure the kid doesn't have physical disabilities like hearing..vision..speech problem. sometimes these
Jharna
continue..
sometimes due to these physical problems..the diagnosis may be misdiagnosed.
treatment for autism.
well it depends on the severity.
since autistic kids have problems in communicating and adopting to the environment.. it's best to expose the child in situations where the child
Jharna
child interact with other kids under doc supervision.
play therapy.
speech therapy.
Engaging in different activities that activate most parts of the brain.. like drawing..painting. matching color board game.
string and beads game.
the more you interact with the child the more effective
Jharna
results you'll get..
please consult a therapist to know what suits best on your child.
and last as a parent. I know sometimes it's overwhelming to guide a special kid.
but trust the process and be strong and patient as a parent.
Jharna
Got questions? Join the online conversation and get instant answers!
Source:
OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5
Google Play and the Google Play logo are trademarks of Google Inc.


