| << Chapter < Page | Chapter >> Page > |
Pendulums are in common usage. Grandfather clocks use a pendulum to keep time and a pendulum can be used to measure the acceleration due to gravity. For small displacements, a pendulum is a simple harmonic oscillator.
A simple pendulum is defined to have a point mass, also known as the pendulum bob , which is suspended from a string of length L with negligible mass ( [link] ). Here, the only forces acting on the bob are the force of gravity (i.e., the weight of the bob) and tension from the string. The mass of the string is assumed to be negligible as compared to the mass of the bob.
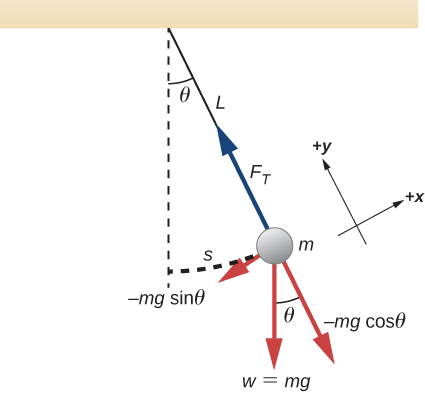
Consider the torque on the pendulum. The force providing the restoring torque is the component of the weight of the pendulum bob that acts along the arc length. The torque is the length of the string L times the component of the net force that is perpendicular to the radius of the arc. The minus sign indicates the torque acts in the opposite direction of the angular displacement:
The solution to this differential equation involves advanced calculus, and is beyond the scope of this text. But note that for small angles (less than 15 degrees), and differ by less than 1%, so we can use the small angle approximation The angle describes the position of the pendulum. Using the small angle approximation gives an approximate solution for small angles,
Because this equation has the same form as the equation for SHM, the solution is easy to find. The angular frequency is
and the period is
The period of a simple pendulum depends on its length and the acceleration due to gravity. The period is completely independent of other factors, such as mass and the maximum displacement. As with simple harmonic oscillators, the period T for a pendulum is nearly independent of amplitude, especially if is less than about Even simple pendulum clocks can be finely adjusted and remain accurate.
Note the dependence of T on g . If the length of a pendulum is precisely known, it can actually be used to measure the acceleration due to gravity, as in the following example.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?