| << Chapter < Page | Chapter >> Page > |
In this chapter we extend the arithmetic and quadratic sequences studied in earlier grades, to geometric sequences. We also look at series, which is the summing of the terms in a sequence.
The simplest type of numerical sequence is an arithmetic sequence .
An arithmetic (or linear ) sequence is a sequence of numbers in which each new term is calculated by adding a constant value to the previous term
For example, is an arithmetic sequence because you add 1 to the current term to get the next term:
| first term: | 1 |
| second term: | 2=1+1 |
| third term: | 3=2+1 |
| term: |
Find the constant value that is added to get the following sequences and write out the next 5 terms.
More formally, the number we start out with is called (the first term), and the difference between each successive term is denoted d , called the common difference .
The general arithmetic sequence looks like:
Thus, the equation for the -term will be:
Given and the common difference, , the entire set of numbers belonging to an arithmetic sequence can be generated.
An arithmetic (or linear ) sequence is a sequence of numbers in which each new term is calculated by adding a constant value to the previous term:
where
A simple test for an arithmetic sequence is to check that the difference between consecutive terms is constant:
This is quite an important equation, and is the definitive test for an arithmetic sequence. If this condition does not hold, the sequence is not an arithmetic sequence.
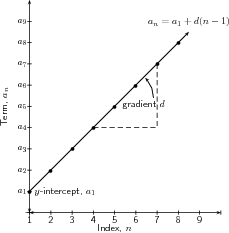
Plotting a graph of the terms of sequence sometimes helps in determining the type of sequence involved.For an arithmetic sequence, plotting vs. results in:
A geometric sequence is a sequence in which every number in the sequence is equal to the previous number in the sequence, multiplied by a constant number.
This means that the ratio between consecutive numbers in the geometric sequence is a constant. We will explain what we mean by ratio after looking at the following example.
Influenza (commonly called “the flu”) is caused by the influenza virus, which infects the respiratory tract (nose, throat, lungs). It can cause mild to severeillness that most of us get during winter time. The main way that the influenza virus is spread is from person to person in respiratory droplets of coughs and sneezes. (This is called “dropletspread”.) This can happen when droplets from a cough or sneeze of an infected person are propelled (generally, up to a metre) through the air and deposited on the mouth or nose of people nearby. Itis good practise to cover your mouth when you cough or sneeze so as not to infect others around you when you have the flu.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 maths' conversation and receive update notifications?