| << Chapter < Page | Chapter >> Page > |
The mean throwing distance of a football for a Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.
Since the problem is about a mean, this is a test of a single population mean.
H 0 : μ = 40
H a : μ >40
p = 0.0062

Because p < α , we reject the null hypothesis. There is sufficient evidence to suggest that the change in grip improved Marco’s throwing distance.
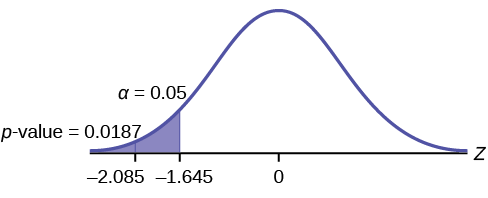
The traditional way to compare the two probabilities, α and the p -value, is to compare the critical value ( z -score from α ) to the test statistic ( z -score from data). The calculated test statistic for the p -value is –2.08. (From the Central Limit Theorem, the test statistic formula is .For this problem, = 16, μ X = 16.43 from the null hypothes is, σ X = 0.8, and n = 15.) You can find the critical value for α = 0.05 in the normal table (see 15.Tables in the Table of Contents). The z -score for an area to the left equal to 0.05 is midway between –1.65 and –1.64 (0.05 is midway between 0.0505 and 0.0495). The z -score is –1.645. Since –1.645>–2.08 (which demonstrates that α> p -value), reject H 0 . Traditionally, the decision to reject or not reject was done in this way. Today, comparing the two probabilities α and the p -value is very common. For this problem, the p -value, 0.0187 is considerably smaller than α , 0.05. You can be confident about your decision to reject. The graph shows α , the p -value, and the test statistics and the critical value.
A college football coach thought that his players could bench press a mean weight of 275 pounds . It is known that the standard deviation is 55 pounds . Three of his players thought that the mean weight was more than that amount. They asked 30 of their teammates for their estimated maximum lift on the bench press exercise. The data ranged from 205 pounds to 385 pounds. The actualdifferent weights were (frequencies are in parentheses)
Conduct a hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds .
Set up the Hypothesis Test:
Since the problem is about a mean weight, this is a test of a single population mean .
H
0 :
μ = 275
H
a :
μ >275
This is a right-tailed test.
Calculating the distribution needed:
Random variable: = the mean weight, in pounds, lifted by the football players.
Distribution for the test: It is normal because σ is known.
pounds (from the data).
σ = 55 pounds (Always use σ if you know it.) We assume μ = 275 pounds unless our data shows us otherwise.
Calculate the p -value using the normal distribution for a mean and using the sample mean as input (see [link] for using the data as input):
.
Interpretation of the p -value: If H 0 is true, then there is a 0.1331 probability (13.23%) that the football players can lift a mean weight of 286.2 pounds or more. Because a 13.23% chance is large enough, a mean weight lift of 286.2 pounds or more is not a rare event.
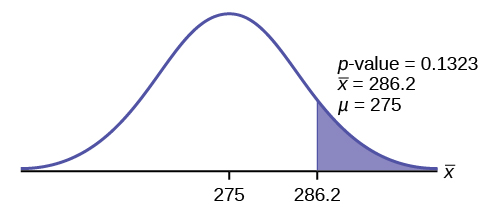
Compare α and the p -value:
α = 0.025 p -value = 0.1323
Make a decision: Since α < p -value, do not reject H 0 .
Conclusion: At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.
The p -value can easily be calculated.

Notification Switch
Would you like to follow the 'Statistics i - math1020 - red river college - version 2015 revision a - draft 2015-10-24' conversation and receive update notifications?