| << Chapter < Page | Chapter >> Page > |
So far we have defined the trig functions using right angled triangles. We can now extend these definitions to any angle. We do this by noting that the definitions do not rely on the lengths of the sides of the triangle, but only on the angle. So if we plot any point on the Cartesian plane and then draw a line from the origin to that point, we can work out the angle of that line. In [link] points P and Q have been plotted. A line from the origin to each point is drawn. The dotted lines show how we can construct right angle triangles for each point. Now we can find the angles A and B.
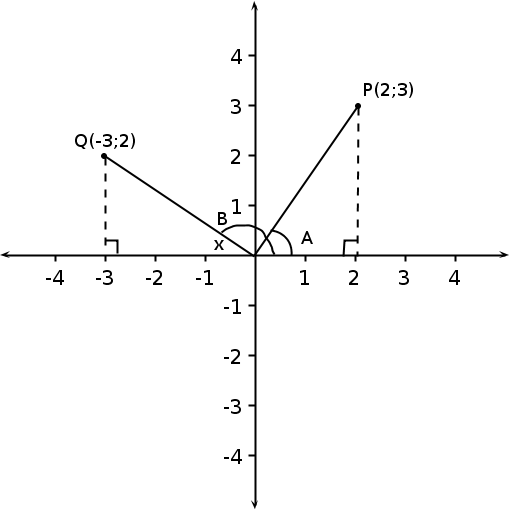
You should find the angle A is . For angle B, you first work out x ( ) and then B is . But what if we wanted to do this without working out these angles and figuring out whether to add or subtract 180 or 90? Can we use the trig functions to do this? Consider point P in [link] . To find the angle you would have used one of the trig functions, e.g. . You should also have noted that the side adjacent to the angle was just the x-co-ordinate and that the side opposite the angle was just the y-co-ordinate. But what about the hypotenuse? Well, you can find that using Pythagoras since you have two sides of a right angled triangle. If we were to draw a circle centered on the origin, then the length from the origin to point P is the radius of the circle, which we denote r. Now we can rewrite all our trig functions in terms of x, y and r. But how does this help us to find angle B? Well, we know that from point Q to the origin is r, and we have the co-ordinates of Q. So we simply use the newly defined trig functions to find angle B! (Try it for yourself and confirm that you get the same answer as before.) One final point to note is that when we go anti-clockwise around the Cartesian plane the angles are positive and when we go clockwise around the Cartesian plane, the angles are negative.
So we get the following definitions for the trig functions:
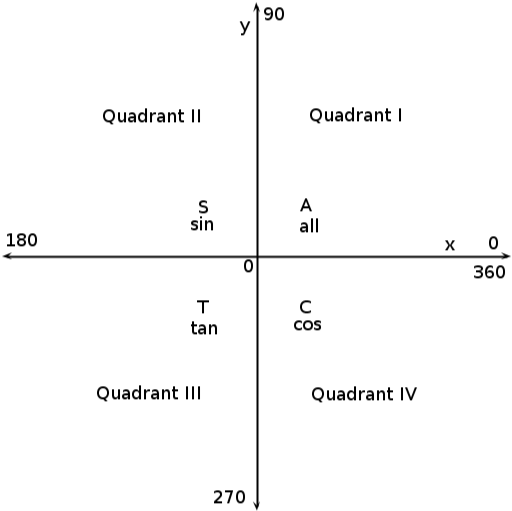
But what if the x- or y-co-ordinate is negative? Do we ignore that, or is there some way to take that into account? The answer is that we do not ignore it. The sign in front of the x- or y-co-ordinate tells us whether or not sin, cos and tan are positive or negative. We divide the Cartesian plane into quadrants and then we can use [link] to tell us whether the trig function is positive or negative. This diagram is known as the CAST diagram.
We can also extend the definitions of the reciprocals in the same way:
Points R(-1;-3) and point S(3;-3) are plotted in the diagram below. Find the angles and .
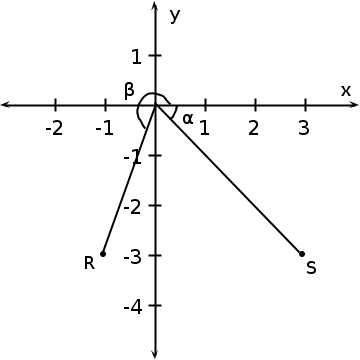
We have the co-ordinates of the points R and S. We are required to find two angles. Angle is positive and angle is negative.
We use tan to find , since we are only given x and y. We note that we are in the third quadrant, where tan is positive.
We use tan to calculate , since we are only given x and y. We also note that we are in the fourth quadrant, where tan is positive.
Angle is and angle is

Notification Switch
Would you like to follow the 'Maths grade 10 rought draft' conversation and receive update notifications?