| << Chapter < Page | Chapter >> Page > |
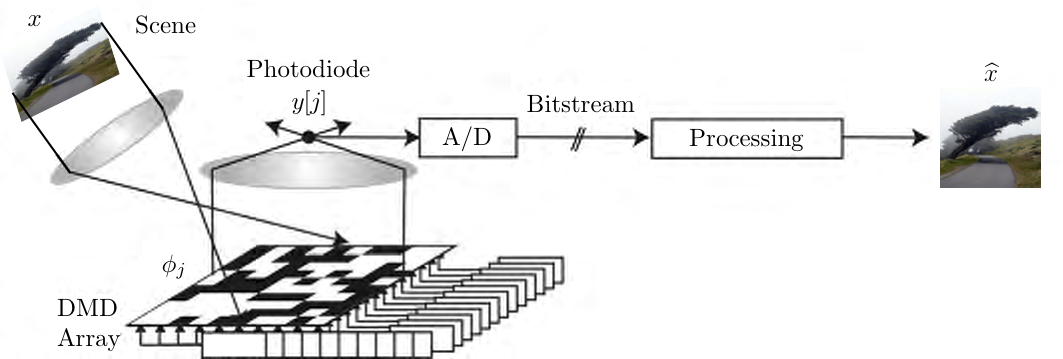
Several hardware architectures have been proposed that apply the theory of compressive sensing (CS) in an imaging setting [link] , [link] , [link] . We will focus on the so-called single-pixel camera [link] , [link] , [link] , [link] , [link] . The single-pixel camera is an optical computer that sequentially measures the inner products between an -pixel sampled version of the incident light-field from the scene under view (denoted by ) and a set of -pixel test functions . The architecture is illustrated in [link] , and an aerial view of the camera in the lab is shown in [link] . As shown in these figures, the light-field is focused by a lens (Lens 1 in [link] ) not onto a CCD or CMOS sampling array but rather onto a spatial light modulator (SLM). An SLM modulates the intensity of a light beam according to a control signal. A simple example of a transmissive SLM that either passes or blocks parts of the beam is an overhead transparency. Another example is a liquid crystal display (LCD) projector.
The Texas Instruments (TI) digital micromirror device (DMD) is a reflective SLM that selectively redirects parts of the light beam. The DMD consists of an array of bacterium-sized, electrostatically actuated micro-mirrors, where each mirror in the array is suspended above an individual static random access memory (SRAM) cell. Each mirror rotates about a hinge and can be positioned in one of two states ( degrees from horizontal) according to which bit is loaded into the SRAM cell; thus light falling on the DMD can be reflected in two directions depending on the orientation of the mirrors.
Each element of the SLM corresponds to a particular element of (and its corresponding pixel in ). For a given , we can orient the corresponding element of the SLM either towards (corresponding to a 1 at that element of ) or away from (corresponding to a 0 at that element of ) a second lens (Lens 2 in [link] ). This second lens collects the reflected light and focuses it onto a single photon detector (the single pixel) that integrates the product of and to compute the measurement as its output voltage. This voltage is then digitized by an A/D converter. Values of between 0 and 1 can be obtained by dithering the mirrors back and forth during the photodiode integration time. By reshaping into a column vector and the into row vectors, we can thus model this system as computing the product , where each row of corresponds to a . To compute randomized measurements, we set the mirror orientations randomly using a pseudorandom number generator, measure , and then repeat the process times to obtain the measurement vector .

Notification Switch
Would you like to follow the 'Introduction to compressive sensing' conversation and receive update notifications?