| << Chapter < Page | Chapter >> Page > |
We now have a much more complex situation. If the waves continue to impinge on the array from one end or the other, the situation will be exactly the sameas when the sensors were on the wire. However, the apparent wavenumber or wavelength of a wave as seen by the array will depend on the angle of attack.
(There is now a difference between the actual wavelength or wavenumber and the apparent wavelength or wavenumber as seen by the array.)
For example, if the wave impinges on the array from a broadside direction, all of the sensors will move up and down in unison regardless of theirseparation and regardless of the actual wavelength of the wave. For this case, the wave will appear to the array to have infinite wavelength or zerowavenumber.
(A linear array has no ability to filter on the basis of wavenumber for waves that impinge on the array from the broadside direction. All wavesfrom that direction appear to have zero wavenumber. This will lead us later to consider the use of a two-dimensional array.)
Figure 4 shows the two-dimensional wavenumber response for a five element linear array with equal weighting for all of the elements. The array is shown atthe top. The wavenumber response of the array is shown at the bottom.
(In this case, I placed all five elements on adjacent points on the space sampling grid with no spaces in between. This places them so close togetherthat you can't visually separate them in the image and they appear as a white line in a black background.)
| Figure 4. The 2D wavenumber response of a linear array. |
|---|
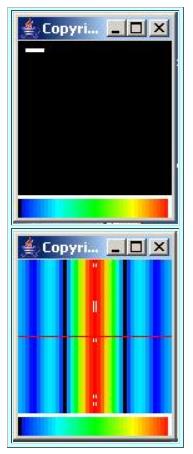 |
If you were to draw a circle centered on the crosshairs (axes) in the center of the wavenumber response, the points on that circle would representa fixed wavenumber for a wave arriving from any direction. The value of the response at any particular point on the circle would indicate the response ofthe array to a wave having that wavenumber from that direction.
If the diameter of the circle is larger than the width of the red vertical band, and if you were to plot that response versus direction, you would see thatthe response is maximum for the two directions that are broadside to the array and the response tends to drop off as the direction approaches the end-firedirection of the array.
You would also notice quite a lot of symmetry. For example, the maximum response occurs in two directions that are 180 degrees apart. In fact, if youpick any direction and a given wavenumber, the response is the same for that direction and for the direction that is 180 degrees around from that direction.
This wouldn't be a very good design for the radio station that I described earlier. If one of the broadside directions of the array faces northeast and theother faces southwest, then the people who live in the northwest and southeast directions wouldn't receive a very good signal from your transmitter. You need adesign that maximizes the power in the four directions where the people live, and that minimizes the power in the other directions. To accomplish that, wewill need a two-dimensional array in place of our one-dimensional linear array.

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?