| << Chapter < Page | Chapter >> Page > |
The gradient has some important properties. We have already seen one formula that uses the gradient: the formula for the directional derivative. Recall from The Dot Product that if the angle between two vectors and is then Therefore, if the angle between and is we have
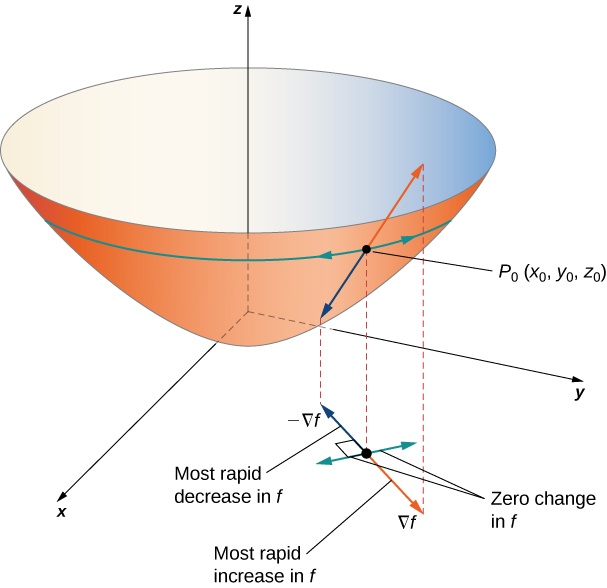
The disappears because is a unit vector. Therefore, the directional derivative is equal to the magnitude of the gradient evaluated at multiplied by Recall that ranges from to If then and and both point in the same direction. If then and and point in opposite directions. In the first case, the value of is maximized; in the second case, the value of is minimized. If then for any vector These three cases are outlined in the following theorem.
Suppose the function is differentiable at ( [link] ).
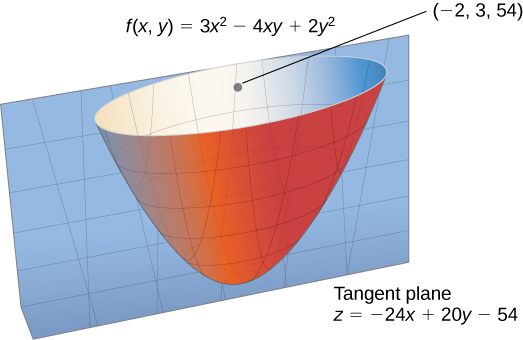
Find the direction for which the directional derivative of at is a maximum. What is the maximum value?
The maximum value of the directional derivative occurs when and the unit vector point in the same direction. Therefore, we start by calculating
Next, we evaluate the gradient at
We need to find a unit vector that points in the same direction as so the next step is to divide by its magnitude, which is Therefore,
This is the unit vector that points in the same direction as To find the angle corresponding to this unit vector, we solve the equations
for Since cosine is negative and sine is positive, the angle must be in the second quadrant. Therefore,
The maximum value of the directional derivative at is (see the following figure).
Find the direction for which the directional derivative of at is a maximum. What is the maximum value?
The gradient of at is The unit vector that points in the same direction as is which gives an angle of The maximum value of the directional derivative is

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?