| << Chapter < Page | Chapter >> Page > |
In Partial Derivatives we introduced the partial derivative. A function has two partial derivatives: and These derivatives correspond to each of the independent variables and can be interpreted as instantaneous rates of change (that is, as slopes of a tangent line). For example, represents the slope of a tangent line passing through a given point on the surface defined by assuming the tangent line is parallel to the x -axis. Similarly, represents the slope of the tangent line parallel to the Now we consider the possibility of a tangent line parallel to neither axis.
We start with the graph of a surface defined by the equation Given a point in the domain of we choose a direction to travel from that point. We measure the direction using an angle which is measured counterclockwise in the x , y -plane, starting at zero from the positive x -axis ( [link] ). The distance we travel is and the direction we travel is given by the unit vector Therefore, the z -coordinate of the second point on the graph is given by
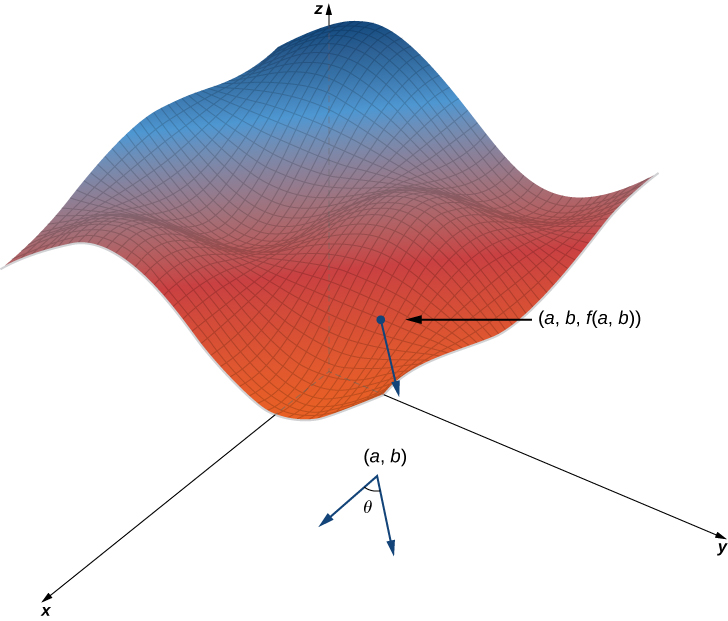
We can calculate the slope of the secant line by dividing the difference in by the length of the line segment connecting the two points in the domain. The length of the line segment is Therefore, the slope of the secant line is
To find the slope of the tangent line in the same direction, we take the limit as approaches zero.
Suppose is a function of two variables with a domain of Let and define Then the directional derivative of in the direction of is given by
provided the limit exists.
[link] provides a formal definition of the directional derivative that can be used in many cases to calculate a directional derivative.
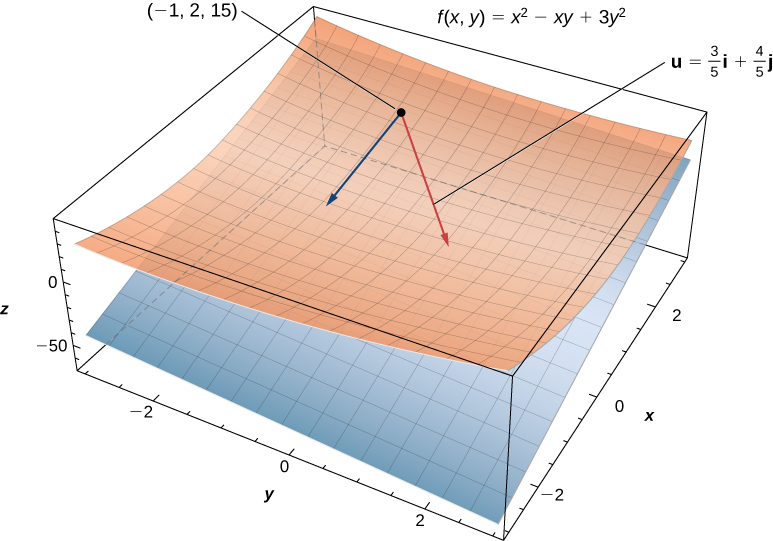
Let Find the directional derivative of in the direction of What is
First of all, since and is acute, this implies
Using we first calculate
We substitute this expression into [link] :
To calculate we substitute and into this answer:
(See the following figure.)

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?