| << Chapter < Page | Chapter >> Page > |
ACTIVITY 1
To compare quadrilaterals for similarities and differences
[LO 3.4]
1. Comparisons
For the next exercise you can form small groups. You are given pairs of quadrilaterals, which you have to compare. Write down in which ways they are alike and in which ways they are different. If you can say exactly by what process you can change the one into the other, then that will show that you have really understood them. For example, look at the question on parallel sides at the end of section 3 above.
Each group should work with at least one pair of shapes. When you work with a kite, you should consider both versions of the kite.
If, in addition, you would like to compare a different pair of quadrilaterals, please do so!
1. Definitions
A very short, but accurate, description of a quadrilateral using the following characteristics, is a definition . This definition is unambiguous, meaning that it applies to one shape and one shape only, and we can use it to distinguish between the different types of quadrilateral.
The definitions are given in a certain order because the later definitions refer to the previous definitions, to make them shorter and easier to understand. There is more than one set of definitions, and this is one of them.
ACTIVITY 2
To develop formulas for the area of quadrilaterals intuitively
[LO 3.4]
Calculating areas of plane shapes .
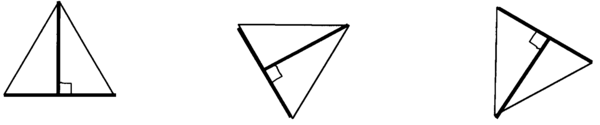

Pick one of the triangles above, and calculate its area three times. Measure the lengths with your ruler, each time using another base/height pair. Do you find that answers agree closely? If they don’t, measure more carefully and try again.

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?