| << Chapter < Page | Chapter >> Page > |
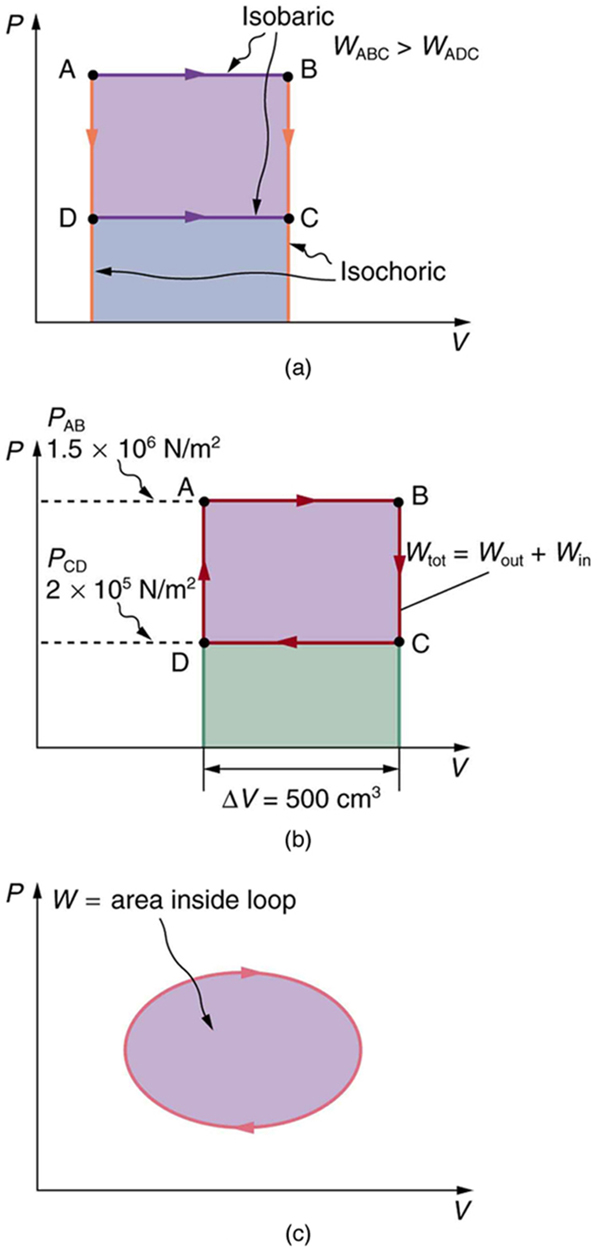
Calculate the total work done in the cyclical process ABCDA shown in [link] (b) by the following two methods to verify that work equals the area inside the closed loop on the diagram. (Take the data in the figure to be precise to three significant figures.) (a) Calculate the work done along each segment of the path and add these values to get the total work. (b) Calculate the area inside the rectangle ABCDA.
Strategy
To find the work along any path on a diagram, you use the fact that work is pressure times change in volume, or . So in part (a), this value is calculated for each leg of the path around the closed loop.
Solution for (a)
The work along path AB is
Since the path BC is isochoric, , and so . The work along path CD is negative, since is negative (the volume decreases). The work is
Again, since the path DA is isochoric, , and so . Now the total work is
Solution for (b)
The area inside the rectangle is its height times its width, or
Thus,
Discussion
The result, as anticipated, is that the area inside the closed loop equals the work done. The area is often easier to calculate than is the work done along each path. It is also convenient to visualize the area inside different curves on diagrams in order to see which processes might produce the most work. Recall that work can be done to the system, or by the system, depending on the sign of . A positive is work that is done by the system on the outside environment; a negative represents work done by the environment on the system.
[link] (a) shows two other important processes on a diagram. For comparison, both are shown starting from the same point A. The upper curve ending at point B is an isothermal process—that is, one in which temperature is kept constant. If the gas behaves like an ideal gas, as is often the case, and if no phase change occurs, then . Since is constant, is a constant for an isothermal process. We ordinarily expect the temperature of a gas to decrease as it expands, and so we correctly suspect that heat transfer must occur from the surroundings to the gas to keep the temperature constant during an isothermal expansion. To show this more rigorously for the special case of a monatomic ideal gas, we note that the average kinetic energy of an atom in such a gas is given by

Notification Switch
Would you like to follow the 'College physics: physics of california' conversation and receive update notifications?