| << Chapter < Page | Chapter >> Page > |
There must be reasons that real macroscopic processes cannot be reversible. We can imagine them going in reverse. For example, heat transfer occurs spontaneously from hot to cold and never spontaneously the reverse. Yet it would not violate the first law of thermodynamics for this to happen. In fact, all spontaneous processes, such as bubbles bursting, never go in reverse. There is a second thermodynamic law that forbids them from going in reverse. When we study this law, we will learn something about nature and also find that such a law limits the efficiency of heat engines. We will find that heat engines with the greatest possible theoretical efficiency would have to use reversible processes, and even they cannot convert all heat transfer into doing work. [link] summarizes the simpler thermodynamic processes and their definitions.
| Isobaric | Constant pressure |
| Isochoric | Constant volume |
| Isothermal | Constant temperature |
| Adiabatic | No heat transfer |
Watch different types of molecules form a solid, liquid, or gas. Add or remove heat and watch the phase change. Change the temperature or volume of a container and see a pressure-temperature diagram respond in real time. Relate the interaction potential to the forces between molecules.

A great deal of effort, time, and money has been spent in the quest for the so-called perpetual-motion machine, which is defined as a hypothetical machine that operates or produces useful work indefinitely and/or a hypothetical machine that produces more work or energy than it consumes. Explain, in terms of heat engines and the first law of thermodynamics, why or why not such a machine is likely to be constructed.
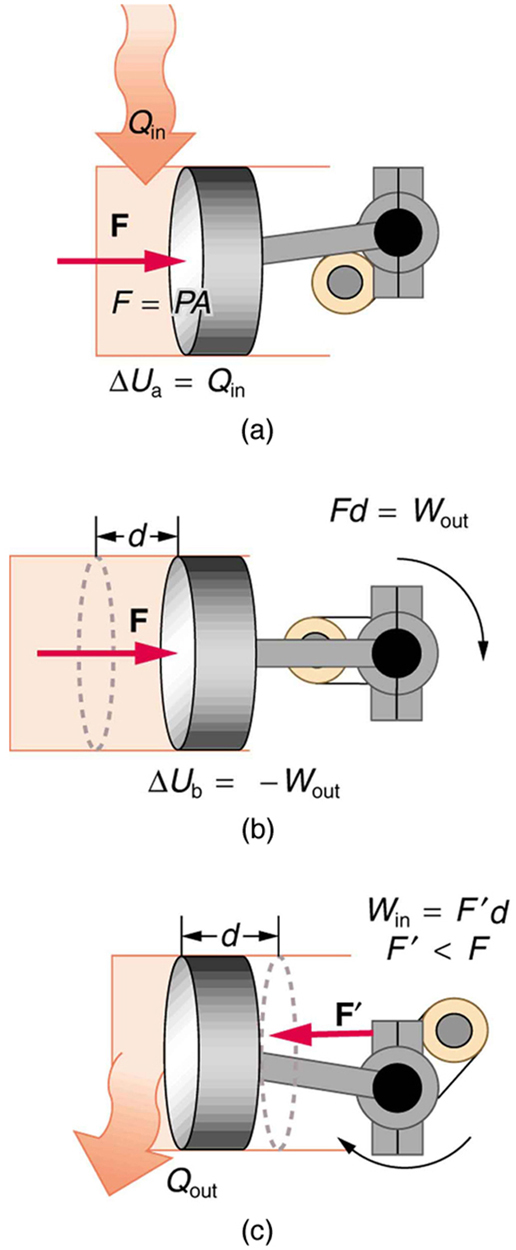
One method of converting heat transfer into doing work is for heat transfer into a gas to take place, which expands, doing work on a piston, as shown in the figure below. (a) Is the heat transfer converted directly to work in an isobaric process, or does it go through another form first? Explain your answer. (b) What about in an isothermal process? (c) What about in an adiabatic process (where heat transfer occurred prior to the adiabatic process)?

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?