| << Chapter < Page | Chapter >> Page > |
Calculate the magnetic field at O for the current loop shown in the figure.
Magnetic field due to current in wire

The magnetic field due to linear part of the wire is zero as they pass through O when extended. The magnetic field due to inner arc is greater than outer arc. Further, magnetic field due to anticlockwise current in the inner arc is out of the plane of drawing and magnetic field due to clockwise current in the outer arc is into the plane of drawing. Net magnetic field due to the current in the wire is out of the plane of drawing, whose magnitude is :
A current of 10 ampere flows in anticlockwise direction through the arrangement shown in the figure. Determine the magnetic field at the center “O”.
Magnetic field due to current in wire

The magnetic field at “O” due to ¾ th of the circular arc is :
Two linear part segments when extended pass through “O” and as such do not contribute to magnetic field. The magnetic field at “O” due to one 5 m segment is :
The magnetic field at “O” due to two 5 m segments is :
Magnetic fields due to both circular arc and linear segments are acting out of the plane of drawing, the net magnetic field at “O” is :
A current of 10 ampere flows in anticlockwise direction through the arrangement shown in the figure. The curved part is a semicircular arc. Determine the magnetic field at the center “O”.
Magnetic field due to current in wire
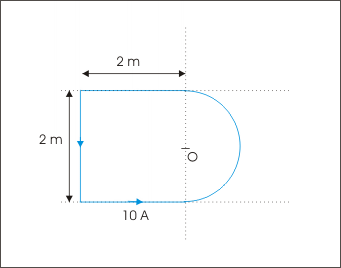
The magnetic field at “O” due to semicircular arc acts upward and its magnitude is :
The magnetic field due to lower straight conductor acts upward and its magnitude is :
The magnetic field due to upper straight conductor acts upward and its magnitude is equal to that due to lower straight conductor :
For the straight conductor at the far end, the center “O” lies on the bisector. The magnetic field acts upward and its magnitude is :
Here, R = 2 m, L = 2 m. Putting values in the equation, we have :
The net magnetic field at “O” is :
A thin disc of radius “R” has uniform distribution of charge, q, on it. The ring is made to rotate at an angular velocity “ω” about an axis passing through its center and perpendicular to its plane. Determine the magnitude of magnetic field at the center of the disc.
We consider disc to be composed of infinite numbers of thin ring. We consider one such ring of thickness dr at a distance “r” from the center carrying charge dq. This ring carrying charge “dq” and rotating is equivalent to a current. The magnetic field at the center to this thin ring is (as obtained earlier in the example problem) :
Magnetic field due to rotating charged disc
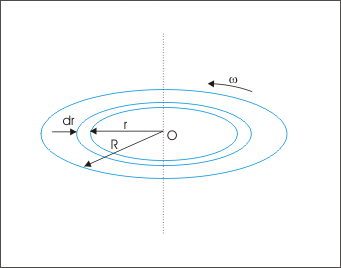
We need to determine “dq” in terms of given parameters. The current surface density, σ, is :
The area of the thin ring is :
Hence, charge on the ring is :
Putting this espression for “dq”, the expression of magnetic field at the center due to rotating ring is :
In order to obtain magnetic field due to the rotating disc, we integrate the expression of magnetic field due to ring from r = 0 to r =R.
Taking out constants out of the integration sign, we have :

Notification Switch
Would you like to follow the 'Electricity and magnetism' conversation and receive update notifications?