| << Chapter < Page | Chapter >> Page > |
We have already determined magnetic field due to current in circular wire at its center. The approach to determine magnetic field at an axial point is similar. We begin with magnetic field due to small current element and then try to integrate the Biot-Savart expression for the small magnetic field for the entire circle following superposition principle.
This extension of earlier procedure, however, demands a bit of extra three dimensional imagination to arrive at the correct result. In this module, we shall attempt to grasp three dimensional elements as clearly as possible with figures. Let us have a look at the differential Biot-Savart expression :
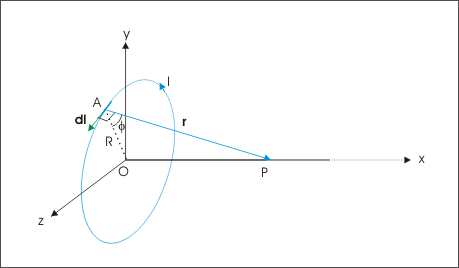
There are three vector quantities d B , d l and r . We investigate the spatial relation among these quantities for magnetic field at an axial point.
The magnitude of magnetic field due to current in a current element is given by :
In order to evaluate magnetic field due to complete circular wire, we need to set up corresponding integral properly with respect to various elements constituting the expression. In following subsections, we study these elements in which point of observation is a point on axial line.
The angle (θ ) as appearing in the Biot-Savart expression between current length element vector d l and displacement vector r is right angle. See figure. This right angle should be distinguished with acute angle φ, which is the angle between OA and AP as shown in the figure.
The angle between current length element and displacement vectors
The above fact reduces Biot-Savart expression to :
This simplification due to enclosed angle being right angle is true for all points on the circle.
All current elements are at equal linear distance from point P. As a result, the magnitude of magnetic field at P due to any of the equal current elements is same.
Unlike enclosed angle (θ), linear distance (r) and magnitude of magnetic field, the direction of magnetic field due to current elements are not same. As such, we can not integrate Biot-Savart differential expression to determine net magnetic field at P. Let us investigate the direction of magnetic fields due to two diametrically opposite current elements. Let the circular wire lie in yz plane as shown in the figure.
Direction of elemental magnetic field

The current length vector and displacement vector form a plane shown as plane 1 and the magnetic field due to current element, , is perpendicular to plane 1. Similarly, the current length vector and displacement vector form a plane shown as plane 2 and the magnetic field due to current element, ), is perpendicular to plane 2. Clearly, these magnetic fields are directed in three dimensional space. If we imagine magnetic fields due to other current elements of the circular wire, then it is not difficult to imagine that these elemental magnetic fields are aligned on the outer surface of a conic section and that they are not in same plane.

Notification Switch
Would you like to follow the 'Electricity and magnetism' conversation and receive update notifications?