12.8 Hyperbolas  (Page 2/2)

$c$ is defined in a very similar way: it goes from the center to either focus.

$b$ is perpendicular to the other two, just as before. But it goes from the center to…well, to a sort of strange point in the middle of nowhere. We’re going to use this point. The distance from the top point to the bottom point ( $2b$ ) is called the conjugate axis.

But here is one major difference. In an ellipse, the foci are inside; in a hyperbola, they are outside. So you can see, just looking at an ellipse, that $a>c$ ; and you can see, just looking at a hyperbola, that $c>a$ . Hence, our equation relating the three shapes is going to be different. Instead of $a^2=b^2+c^2$ , we have $c^2=a^2+b^2$ . This reflects the fact that c is the biggest one in this case.

Once again, the class should be able to see that if the center is ( $h$ , $k$ ) instead of the origin, we replace $x^2$ with $(x-h{)}^2$ and $y^2$ with $(y-k{)}^2$ .

How about a vertical hyperbola? That looks like this:

The way we tell vertical from horizontal is completely different. In an ellipse, we told by assuming that $a>b$ . In a hyperbola, we have no such guarantee; either $a$ or $b$ could be the greater, or they could even be the same. Instead, we look at which one comes first. If we are doing an $x^2-y^2$ thing, it’s horizontal; if we are doing a $y^2-x^2$ thing, it’s vertical. This is a very common source of errors…be careful!

There should be no need to go through the whole completing-the-square rigmarole on the board—just tell them it is exactly like with ellipses, including making sure you have a 1 on the right, and there is nothing multiplied by $x^2$ or $y^2$ . But the really different part is the graphing. So let’s just pick it up there. Suppose you want to graph:

$\frac{{\left(x-2\right)}^2}{\text{36}}-\frac{(y+3{)}^2}{4}=1$

First of all, what is the center? That’s easy: (2,-3).

Now, here is a harder question: does it open vertically, or horizontally? We can answer this question without even looking at the numbers on the bottom! The $x^2$ is positive and the $y^2$ is negative, so this is horizontal.

As we did with ellipses, we will then find $a$ , $b$ , and $c$ . $a=6$ and $b=2$ . We will find c with the hyperbola equation $c^2=a^2+b^2$ (different from the ellipse equation!) and get $c=\sqrt{\text{40}}$ which is $2\sqrt{\text{10}}$ or somewhere just above 6 (again, because 40 is just above 36).

Now, it’s drawing time. We start at the center. We go out horizontally by 6 to find the vertices, and by a little more than 6 to find the foci. We go out vertically by 2 to find the endpoints of the conjugate axis, those weird little points in space. Then what?

Here’s what you do. Draw a rectangle, going through the vertices, and the endpoints of the conjugate axis. Then, draw diagonal lines through the corners of that rectangle. Those diagonal lines are going to serve as asymptotes, or guides: they are not part of the hyperbola, but they help us draw it. Why? Because as it moves out, the hyperbola gets closer and closer to the asymptotes, but never quite reaches them. So once you have drawn your asymptotes, you have a guide for drawing in your hyperbola.

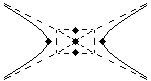
Note that I draw the box and the asymptotes in dotted lines, indicating that they are not really part of the hyperbola.

It’s worth talking for a while about what an asymptote is, since it is such an important concept in Calculus—the line that the curve gets closer and closer and closer to, without ever quite reaching. It’s also worth pointing out that this shows that a hyperbola is not two back-to-back parabolas, since parabolas do not display asymptotic behavior.

Finally, I always mention the comet again. Remember that if a comet comes in with high energy, it swoops around the sun and then flies away again. Now, if there were no sun—if there were nothing in the universe but our comet—the comet would travel in a straight line. And clearly, when the comet is very, very far away from the sun (either before or after its journey through our solar system), the effect of the sun is very small, so the comet travels almost in a straight line. That straight line is the asymptote. The farther away from the sun the comet gets, the closer it gets to that straight line.

Homework:

The only really unusual thing here is that I ask for the equation of one of the asymptotes. This is just a quick review of the skill of finding the equation for a line, given that you already know two points on the line.

You will note that I have absolutely nothing here about going from the geometry of the hyperbola, to the equation. The reason is that it is exactly like the ellipse. You may want to do it, or you may not. If you do it, you shouldn’t need to hand them anything—just say “By analogy to what we did with the ellipse, do this.”

Now that you have done all the shapes, the one vital skill that cuts across all of it is looking at an equation ( $a{x}^2+b{y}^2+cx+dy+e=0$ ) and telling what shape it is. This is done entirely by looking at the coefficients of the squared terms ( $a$ and $b$ ), and you should refer them to the chart at the end of the “Conceptual Explanations.”

Time for our very last test!

With luck, you have two or three weeks left for review after this, before the final test. Congratulations, you made it through!