| << Chapter < Page | Chapter >> Page > |
The good news about hyperbolas is, they are a lot like ellipses—a lot of what has already been learned, will come in handy here. The bad news about hyperbolas is, they are a lot like ellipses—so all the little differences can be very confusing.
We will start as always with the geometric definition. Let them do the assignment “Distance to this point minus distance to that point is constant” in groups, and help them out until they get the shape themselves. There are two pretty easy points to find on the -axis, but from there they just sort of have to noodle around like we did with parabolas, asking…what happens as I move inside? What happens as I move outside? As always, keep wandering and hinting until most groups have drawn something like a hyperbola. Then you lecture.
The lecture starts by pointing out what we have. We have two points, once again called the foci. They are the defining points of the hyperbola, but they are not part of the hyperbola. And we also once again have a distance which is part of the definition.
Because the foci were horizontally across from each other, we have a horizontal hyperbola. If they were vertically lined up, we would have a vertical hyperbola. You can also do diagonal hyperbolas—anyone remember where we have seen one of those? That’s right, inverse variation! That was a hyperbola, just like these. But we’re not going to talk about those in this unit, just the horizontal and vertical ones.
Incidentally, a hyperbola is not two back-to-back parabolas. It looks like it, but these shapes are actually different from parabolic shapes, as we will see.
OK, so, what good are hyperbolas? The analogy continues…orbits! Suppose a comet is heading toward the sun. (Draw.) If it has a low energy—that is, a low velocity—it gets trapped by the sun, and wins up orbiting around the sun in an elliptical orbit. But if it has high energy (high velocity) it zooms around the sun and then zooms away forever. Its path in this case is half a hyperbola.
Another cool use is in submarine detection. A submarine sends out a pulse. Two receiving stations get the pulse. They don’t know what direction it came from or when it was sent, but they do know that one station received it exactly two seconds before the other one. This enables them to say that the distance from the sub to this station, minus the distance to this other station, is such-and-such. And this, in turn, locates the sub on a hyperbola.
OK, on to the machinery. Here is the equation for a horizontal hyperbola, centered at the origin.
Looks familiar, doesn’t it? But the plus has changed to a minus, and that makes all the difference in the world.
Here is a drawing of a horizontal hyperbola.
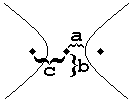
Let’s be very careful in seeing how this is, and is not, like an ellipse.
a is defined in a very similar way. It goes from the center, to the edges. In this case, the edges are called the “vertices” (in analogy to parabolas). The distance from one vertex to the other ( of course) is called the transverse axis.

Notification Switch
Would you like to follow the 'Advanced algebra ii: teacher's guide' conversation and receive update notifications?