| << Chapter < Page | Chapter >> Page > |
ALGEBRA
CLASS ASSIGNMENT 1
Look at the polynomial, for example
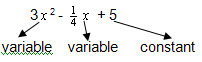
From the above, you will be able to recognise the following:
Here you have it:
1. Study the following in your groups and supply the answers:
1.1 number of terms
1.2 coefficient of
1.3 constant
1.4 degree of the expression
2. Now we can use variables to define the following with the magical language of mathematics --- i.e. algebraic expressions.
See if you can define these in the form of algebraic expressions:
Given Algebraic Expression
2.1 The sum of a number and 9
2.2 A number multiplied by 7
2.3 The difference between a and b
2.4 6 less than a number reduced by 7
2.5 The product of a number and b
2.6 Quotient of a number and 7
2.7 Square of a
2.8 Square root of a
2.9 Subtract the difference between a and b from their product
3. The following are referred to as flow diagrams – They consist ofa) inputb) formula in which the input number is substitutedc) output
Complete (a), (b) and (c)

4. See if you can determine a formula for the following and complete the table.
| 2 | 5 | 8 | 10 | 15 | 47 | |
| y | 7 | 11 | 17 |
formula: y =
HOMEWORK ASSIGNMENT 1
1. Determine a formula for each of the following and complete the table.
1.1 formula: y = ……………………………………………………
| 2 | 5 | 8 | 9 | 12 | 20 | |
| y | 10 | 16 | 22 |
1.2 formula: y = ……………………………………………………
| 3 | 7 | 10 | 9 | 12 | 20 | |
| y | 12 | 32 | 47 |
1.3 formula: y = ……………………………………………………
| 1 | 3 | 4 | 9 | 12 | 20 | |
| y | 1 | 9 | 16 |
1.4 formula: y = ……………………………………………………
| 1 | 2 | 3 | 6 | 7 | 10 | |
| y | 1 | 8 | 27 |
1.5 formula: y = ……………………………………………………
| 1 | 2 | 4 | 9 | 12 | 20 | |
| y | 2 | 5 | 17 |
2. The sketch shows matches arranged to form squares and combinations of squares.

2.1 Make a sketch to show four squares and indicate how many matches were used.
Matches? …………………………
2.2 Can you determine a formula that will provide a quick way for determining how many matches you will need to form ( ) number of squares?
y = ………………………………… (with y representing the number of matches)
2.3 Now make use of your formula to determine how many matches you will need to form 110 squares.
2.4 Determine how many squares you will be able to form with 2 005 matches.
3. Examine the following expression and answer the questions that follow:
3.1 Arrange the expression in ascending powers of a.
3.2 Determine:
3.2.1 number of terms
3.2.2 coefficient of a ²
3.2.3 degree of the expression
3.2.4 constant term

Notification Switch
Would you like to follow the 'Mathematics grade 8' conversation and receive update notifications?