| << Chapter < Page | Chapter >> Page > |
Think about twin brothers Andy and Bobby. They are years old. How old was Andy years ago? He was years less than so his age was or What about Bobby’s age years ago? Of course, he was also. Their ages are equal now, and subtracting the same quantity from both of them resulted in equal ages years ago.
Solve:
We will use the Subtraction Property of Equality to isolate
|
| |
| Subtract 8 from both sides. |
|
| Simplify. |
|
|
| |
|
| |
|
|
Since makes a true statement, we know is the solution to the equation.
Solve:
To solve an equation, we must always isolate the variable—it doesn’t matter which side it is on. To isolate
we will subtract
from both sides.
|
| |
| Subtract 74 from both sides. |
|
| Simplify. |
|
Substitute
for
to check.
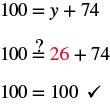 |
Since makes a true statement, we have found the solution to this equation.
In all the equations we have solved so far, a number was added to the variable on one side of the equation. We used subtraction to “undo” the addition in order to isolate the variable.
But suppose we have an equation with a number subtracted from the variable, such as We want to isolate the variable, so to “undo” the subtraction we will add the number to both sides.
We use the Addition Property of Equality, which says we can add the same number to both sides of the equation without changing the equality. Notice how it mirrors the Subtraction Property of Equality.
For any numbers and if
then
Remember the twins, Andy and Bobby? In ten years, Andy’s age will still equal Bobby’s age. They will both be
We can add the same number to both sides and still keep the equality.
Solve:
We will use the
Addition Property of Equality to isolate the variable.
|
| |
| Add 5 to both sides. |
|
| Simplify. |
|
|
|
|
|
|
|
|
|
|
|
|
Solve:
We will add
to each side to isolate the variable.
|
| |
| Add 16 to each side. |
|
| Simplify. |
|
|
|
|
|
| |
|
|
The solution to is
Remember, an equation has an equal sign between two algebraic expressions. So if we have a sentence that tells us that two phrases are equal, we can translate it into an equation. We look for clue words that mean equals . Some words that translate to the equal sign are:
It may be helpful to put a box around the equals word(s) in the sentence to help you focus separately on each phrase. Then translate each phrase into an expression, and write them on each side of the equal sign.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?