| << Chapter < Page | Chapter >> Page > |
Solution for (a)
We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is . We are given the elapsed time, and so . The unknown is acceleration, which can be found from its definition:
Substituting the known values yields
Discussion for (a)
This is an attainable acceleration for an athlete in good condition.
Solution for (b)
Here we are asked to find the average force the player exerts backward to achieve this forward acceleration. Neglecting air resistance, this would be equal in magnitude to the net external force on the player, since this force causes his acceleration. Since we now know the player’s acceleration and are given his mass, we can use Newton’s second law to find the force exerted. That is,
Substituting the known values of and gives
Discussion for (b)
This is about 50 pounds, a reasonable average force.
This worked example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to identify the physical principles involved in the problem. The second step is to solve for the unknown using familiar problem-solving strategies. These strategies are found throughout the text, and many worked examples show how to use them for single topics. You will find these techniques for integrated concept problems useful in applications of physics outside of a physics course, such as in your profession, in other science disciplines, and in everyday life. The following problems will build your skills in the broad application of physical principles.
To simulate the apparent weightlessness of space orbit, astronauts are trained in the hold of a cargo aircraft that is accelerating downward at . Why will they appear to be weightless, as measured by standing on a bathroom scale, in this accelerated frame of reference? Is there any difference between their apparent weightlessness in orbit and in the aircraft?
A cartoon shows the toupee coming off the head of an elevator passenger when the elevator rapidly stops during an upward ride. Can this really happen without the person being tied to the floor of the elevator? Explain your answer.
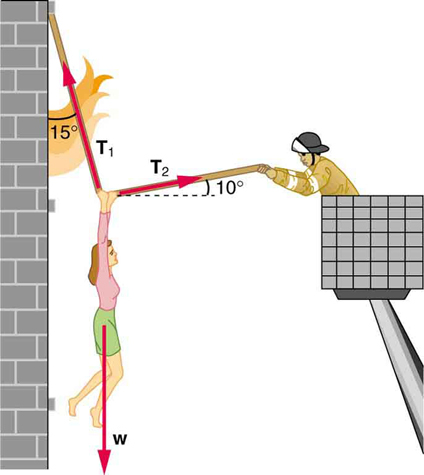
A 76.0-kg person is being pulled away from a burning building as shown in [link] . Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.
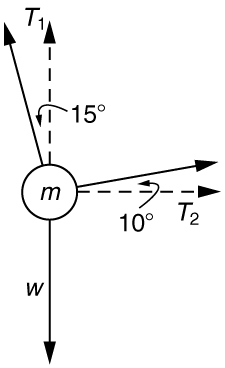
Integrated Concepts When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s. (a) What is his final speed? (b) How far does he travel?
(a)
(b) 2.97 m
Integrated Concepts A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor. (a) Calculate his velocity when he leaves the floor. (b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in part (a) in a distance of 0.300 m. (c) Calculate the force he exerts on the floor to do this, given that his mass is 110 kg.
(a)
(b)
(c)
Unreasonable Results A 75.0-kg man stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s. (a) Calculate the scale reading in newtons and compare it with his weight. (The scale exerts an upward force on him equal to its reading.)

Notification Switch
Would you like to follow the 'Newton's laws' conversation and receive update notifications?