| << Chapter < Page | Chapter >> Page > |
For such situation involving nonlinear wire, we prefer to have an expression for a infinitesimally small length of wire. This consideration of very small length of wire guarantees that the wire element is straight. Following the similar argument as for a straight wire, the magnetic force on an infinitesimally small length of wire is :
We can, then, use this expression and integrate along non-linear wire. Of course, such calculation will depend on the possibility to divide the given wire into segments for which integration of this expression is possible.
We have pointed out the equivalent role of current element and moving charge in the context of production or setting up of magnetic field. An inspection of the expression of magnetic force on a charge and a current element indicate that the equivalence is true also in the case of experiencing magnetic force. In the case of moving charge, the magnetic force is given by :
On the other hand, the magnetic force on a small current carrying wire element is :
Clearly, the term “q v ” and “Id L ” play the equivalent role in two cases.
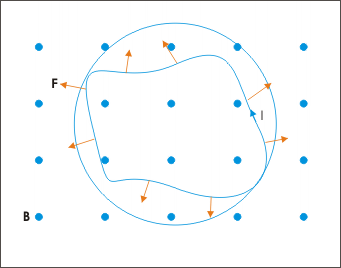
Problem : An irregular shaped flexible wire loop of length “L” is placed in a perpendicular and uniform magnetic field “B” as shown in the figure below (The magnetic force represented by filled circle is perpendicular and out of the plane of drawing). Determine the tension in the loop if a current “I” is passed through it in anticlockwise direction.
An irregular shaped flexible wire loop in magnetic field

Solution : The wire loop is flexible. There would be tension, provided the loop elements experience magnetic force in outward direction at all points on it. Applying Right hand thumb rule for any small segment of the loop, we find that the wire is indeed subjected to outward magnetic force. Clearly, the loop expands to become a circular loop. The radius of the circle is given by :
An irregular shaped flexible wire loop in magnetic field
In order to determine tension in the wire, we consider a very small element of the circular loop. Let the loop element subtends an angle dθ at the center. Let “T” be the tension in the wire. It is clear that components of tension in the downward direction should be equal to magnetic force on the small wire element.
The tension in the circular loop carrying current

Since loop element is very small, we approximate as :
Further, we can consider the small loop element to be a straight wire for the calculation of magnetic force. Now, the magnetic force on the loop element is :
Substituting in the equilibrium equation,
Again substituting for the radius of circle, we have :
The situation here is just an extension of the study of the magnetic force on a current carrying wire. The basic consideration here is that a wire carrying current can function in either of following two roles : (i) it produces magnetic field and (ii) it experiences magnetic force.

Notification Switch
Would you like to follow the 'Electricity and magnetism' conversation and receive update notifications?