| << Chapter < Page | Chapter >> Page > |
ʼn Vierkant is ʼn rombus met al vier sye ewe lank en al vier hoeke gelyk aan 90 .
ʼn Opsomming van die eienskappe van ʼn vierkant:

ʼn Vlieër is ʼn vierhoek met twee pare aangrensende sye ewe lank.
ʼn Oposmming van die eienskappe van ʼn vlieër is:

Reghoeke is ʼn spesiale geval (ʼn deelversameling) van die parallelogramme. Reghoeke is parallelogramme met alle hoeke regte hoeke. Vierkante is ʼn spesiale geval (deelversameling) van die reghoeke. Vierkante is reghoeke met al vier sye ewe lank. So, alle vierkante is parallelogramme én reghoeke. As jy gevra word om te bewys dat ʼn vierhoek ʼn parallelogram is, is dit genoeg om aan te toon dat beide pare teenoorstaande sye parallel is. Maar, as jy gevra word om te bewys dat ʼn vierhoek ʼn vierkant is, dan moet jy ook wys dat al die hoeke regte hoeke is én dat al die sye ewe lank is.
Veelhoeke is oral rondom ons. ʼn Stopteken het die vorm van ʼn agthoek, m.a.w. ʼn agthoekige veelhoek. Die heuningkoek van ʼn bynes bestaan uit heksagonale selle. Die oppervlak van ʼn tafel is dikwels ʼn reghoek.
In hierdie afdeling sal jy leer van gelykvormige veelhoeke.
Gebruik die diagram om die tabel in te vul en beantwoord die vrae wat daarop volg.
| = | =... | ... |
| = | =... | =... |
| = | ... | =... |

As twee veelhoeke gelykvormig is, is die een ʼn vergroting van die ander. Dit beteken dat die veelhoeke dieselfde grootte hoeke sal hê en dat hulle sye in verhouding tot mekaar sal wees.
Die simbool wat ons gebruik om gelykvormigheid aan te dui is .
Twee veelhoeke is gelykvormig as:
Bewys dat die volgende twee veelhoeke gelykvormig is.

Daar word gevra om te bewys dat ʼn paar veelhoeke gelykvormig is. Ons kan dit doen deur te bewys dat die verhouding van ooreenstemmende sye gelyk is en dat die ooreenstemmende hoeke ewe groot is.
Die hoeke en hul groottes word gegee, so ons kan bewys dat hulle ewe groot is.
Al die hoeke is 90 groot en
Eerstens moet ons kyk watter sye ooreenstem. Die reghoeke het twee lang sye wat gelyk is en twee kort sye wat gelyk is. Ons moet die verhoudings van die lang sye van die twee reghoeke vergelyk en ons moet die verhoudings van die kort sye vergelyk.
Lang sye, groot reghoek se waardes op die klein reghoek se waardes:
Kort sye, groot reghoek se waardes op die klein reghoek se waardes:
Die verhouding van die ooreenstemmende sye is gelyk, twee in hierdie geval.
Die ooreenstemmende hoeke is ewe groot en die verhoudings van die ooreenstemmende sye is gelyk, dus is dieveelhoeke ABCD en EFGH gelykvormig.
As twee vyfhoeke ABCDE en GHJKL gelykvormig is, bepaal die lengtes van die sye en die groottes van die hoeke wat met letters gemerk is:
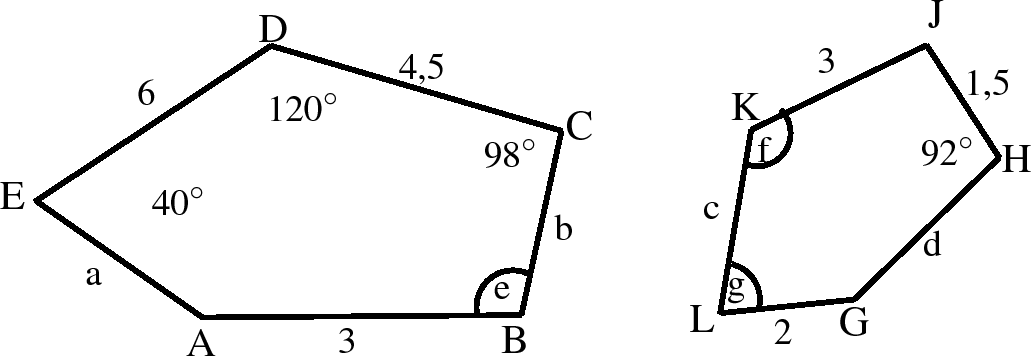
Daar word aan ons gegee dat ABCDE en GHJKL gelykvormig is. Dit beteken dat:
en
Daar word gevra om te bepaal
Die ooreenstemmende hoeke is ewe groot en daar is dus geen berekening nodig nie. Daar word aan ons ʼn paar sye en gegee wat ooreenstemmend is. so ons weet dat al die sye van 1,5 keer kleiner is as die sylengtes van .
Werk in pare en toon dat alle gelyksydige driehoeke gelykvormig is.


Ondersoek verskillende maniere om poligone te definieer. Jy behoort spesiale aandag te gee aan die volgende poligone:
Neem in oorweging hoe die figure in hierdie boek gedefinieer is en watter alternatiewe definisies daar bestaan. Byvoorbeeld, ʼn driehoek is ʼn driesydige poligoon of ʼn driehoek is ʼn figuur met drie sye en drie hoeke. Driehoeke kan geklassifiseer word volgende hulle sye of volgens hulle hoeke. Kan mens ook vierhoeke op hierdie manier klassifiseer? Watter ander name is daar vir hierdie figure? Byvoorbeeld, vierhoeke kan ook genoem word tetragone.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?