| << Chapter < Page | Chapter >> Page > |
A graph is a set with a set of vertices and a set of edges or vertex pairs. Two vertices are adjacent if the vertex pair are in . Graphs are a common model for networks.

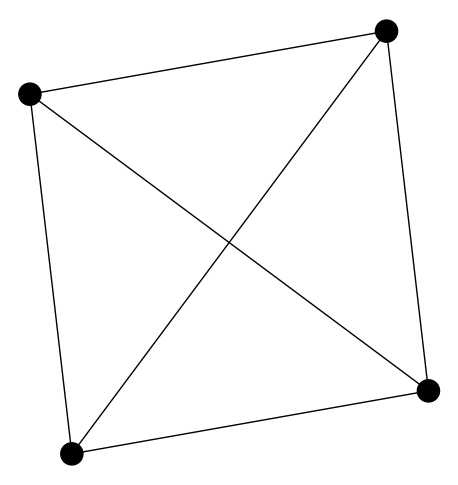
A graph G on vertices is a complete graph if for each pair . Call the complete graph on vertices.
Given graphs and the Cartesian Product Graph is defined to be with

Given a graph and a set then we define the neighbors of to be the set
and similarly the closed neighborhood is the set
Given a graph , a set is a dominating set if .
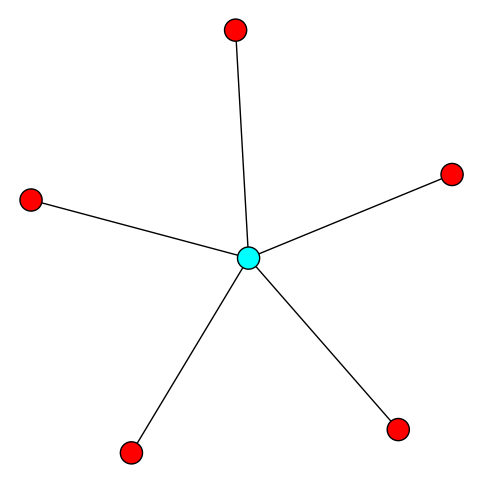
Given a graph , the domination number of is
A graph , is called k-edge-critical (or k-critical , for short) if , and, such that and are not adjacent, .
Given a graph , a set is independent if for all . An independent set is maximal if it is not a subset of any other independent set.

Given a graph , the independence number denoted is defined by
Domination Theory is an emerging field in Graph Theory addressing how to find dominating sets for certain graphs and important models in the theory.
Domination Theory is a very interesting subfield of graph theory because it has many real-world applications. Finding a minimum set whose closed neighborhood encompasses a network has obvious implications for minimum-cost ways of altering a network, or cheaply distributing goods throughout a network. For example, dominating set theory can help cell phone companies place a minimum number of towers to insure coverage for all of its clients. Similarly, dominating set theory can be useful for social marketing, in order to succesfully spread news about a product by using a minimal number of advertisements. In a less business-minded view, domination theory can help modeling the squares which are connected by the moves of a chess piece (such as the queen). This can be useful for solving problems like the maximum-placement problem, for an arbitary chess board, or for pieces with different movements. Lastly, domination theory can also have applications in facility location problems, such as finding the minimum distance to travel to one out of a set of locations (such as a police station). [link]

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?