| << Chapter < Page | Chapter >> Page > |
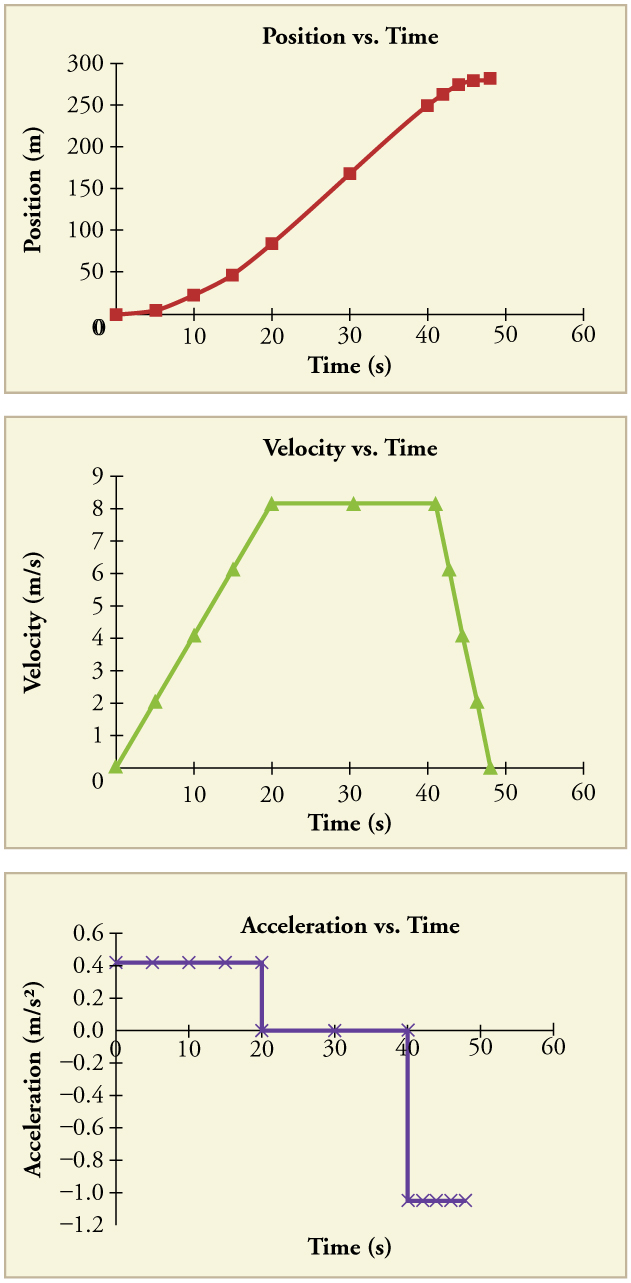
The graphs of position, velocity, and acceleration vs. time for the trains in [link] and [link] are displayed in [link] . (We have taken the velocity to remain constant from 20 to 40 s, after which the train decelerates.)
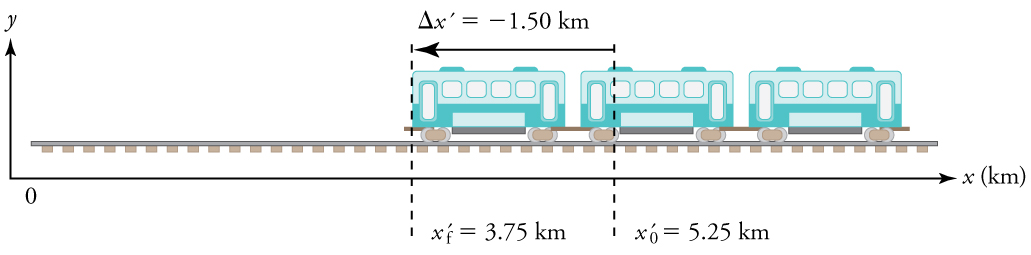
What is the average velocity of the train shown below, if it takes 5.00 min to make its trip?
Strategy
Average velocity is displacement divided by time. It will be negative here, since the train moves to the left and has a negative displacement.
Solution
1. Identify the knowns. , , .
2. Determine displacement, . We found to be
3. Solve for average velocity.
4. Convert units.
Discussion
The negative velocity indicates motion to the left.
Perhaps the most important thing to note about these examples is the signs of the answers. In our chosen coordinate system, plus means the quantity is to the right and minus means it is to the left. This is easy to imagine for displacement and velocity. But it is a little less obvious for acceleration. Most people interpret negative acceleration as the slowing of an object. In fact, a negative acceleration will increase a negative velocity. For example, the train moving to the left could speed up by an acceleration to the left. In this case, both and are negative. The plus and minus signs give the directions of the accelerations. If acceleration has the same sign as the velocity, the object is speeding up. If acceleration has the opposite sign as the velocity, the object is slowing down.
An airplane lands on a runway traveling east. Describe its acceleration.
If we take east to be positive, then the airplane has negative acceleration, as it is accelerating toward the west. It is also decelerating: its acceleration is opposite in direction to its velocity.
Is it possible for speed to be constant while acceleration is not zero? Give an example of such a situation.
Is it possible for velocity to be constant while acceleration is not zero? Explain.
Give an example in which velocity is zero yet acceleration is not.
If a subway train is moving to the left (has a negative velocity) and then comes to a stop, what is the direction of its acceleration? Is the acceleration positive or negative?
A cheetah can accelerate from rest to a speed of 30.0 m/s in 7.00 s. What is its acceleration?
A commuter backs her car out of her garage with an acceleration of . (a) How long does it take her to reach a speed of 2.00 m/s? (b) If she then brakes to a stop in 0.800 s, what is her acceleration?

Notification Switch
Would you like to follow the 'Kinematics' conversation and receive update notifications?