| << Chapter < Page | Chapter >> Page > |
In this chapter, you will learn to:
In this section, we will consider types of problems that involve a sequence of trials, where each trial has only two outcomes, a success or a failure. These trials are independent, that is, the outcome of one does not affect the outcome of any other trial. Furthermore, the probability of success, , and the probability of failure, , remains the same throughout the experiment. These problems are called binomial probability problems. Since these problems were researched by a Swiss mathematician named Jacques Bernoulli around 1700, they are also referred to as Bernoulli trials .
We give the following definition:
The probability model that we are about to investigate will give us the tools to solve many real-life problems like the ones given below.
We now consider the following example to develop a formula for finding the probability of successes in n Bernoulli trials.
A baseball player has a batting average of . If he bats four times in a game, find the probability that he will have
Let us suppose denotes that the player gets a hit, and denotes that he does not get a hit.
This is a binomial experiment because it meets all four conditions. First, there are only two outcomes, or . Clearly the experiment is repeated four times. Lastly, if we assume that the player's skillfulness to get a hit does not change each time he comes to bat, the trials are independent with a probability of of getting a hit during each trial.
We draw a tree diagram to show all situations.
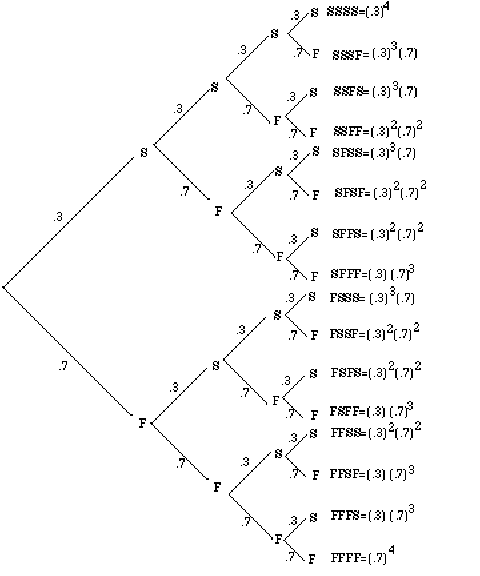
Let us first find the probability of getting, for example, two hits. We will have to consider the six possibilities, , , , , , , as shown in the above tree diagram. We list the probabilities of each below.
Since the probability of each of these six outcomes is , the probability of obtaining two successes is .
The probability of getting one hit can be obtained in the same way. Since each permutation has one and three 's, there are four such outcomes: , , , and .
And since the probability of each of the four outcomes is , the probability of getting one hit is .
The table below lists the probabilities for all cases, and shows a comparison with the binomial expansion of fourth degree. Again, denotes the probability of success, and the probability of failure.
| Outcome | Four Hits | Three hits | Two Hits | One hits | No Hits |
| Probability |

Notification Switch
Would you like to follow the 'Applied finite mathematics' conversation and receive update notifications?