| << Chapter < Page | Chapter >> Page > |

In general, the platonic solids are symmetric across their bisecting planes.
If we can show that the Regular Triangular Prism can be obtained from an arbitrary polyhedron with unit volume through this symmetrization with bisecting planes, then we would show that the Regular Triangular Prism is a solution to Melzak's Problem, given the existence of a solution. Hence, it is unfortunate that the Platonic Solids are already symmetric. We thereby consider the following operation on a polyhedron P with unit volume. Take a plane H that bisect the volume of Then choosing one of the two halves P 1 and P 2 of we merge P j with itself along any face that does not create new edges along the merging face. This method allows one to create distinct polyhedra even if P is already symmetric about all bisecting planes. For example, the cube can be made into a triangular prism consisting of three squares and an isosceles triangle:

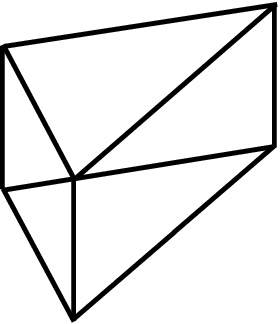
The method of symmetrization remains to be fully explored. Specifically, given a polyhedra P which is symmetric across a plane we ask if a comparison of the edge length of P can be made to the prism formed by the cross section This may involve introducing variations of polyhedra in order to show that near the slice, a prism is optimal.
For the method of variations of polyhedra, we must investigate whether pseudo-minimizers have any special properties, or perhaps show that the only pseudo-minimizers are known polyhedra such as the platonic solids and the right regular prisms. One may show that prisms or right prisms are more efficient that all other figures, since it has already been shown that the Regular Triangular Prism is best among prisms. However, it would be easier to show that the Regular Triangular Prism in particular is more efficient than all other figures instead of considering an arbitrary right prism; hence the classical approach of pointing out improvements to large classes of polyhedra (aside from prisms) may not be effective. A non-variational approach may be more promising.
A computational approach using technology also remains to be taken. We seek to write a computer program to bisect and then reflect polyhedra, and then perhaps take variations. Thus far, our only use of computers has been to plot the graphs of for a variation P t for a given polyhedron
This report summarizes work done as part of the Calculus of Variations PFUG under Rice University's VIGRE program. VIGRE is a program of Vertically Integrated Grants for Research and Education in the Mathematical Sciences under the direction of the National Science Foundation. A PFUG is a group of Postdocs, Faculty, Undergraduates and Graduate students formed round the study of a common problem.
This module introduces an overview of Melzak's Problem, and discusses two methods for studying the problem: the method of Variations and the method of Symmetrization. Examples of each method applied to the cube and the Regular Triangular Prism are presented, and a discussion on future directions is provided.
This Connexions module describes work conducted as part of Rice University's VIGRE program, supported by National Science Foundation grant DMS-0739420. We would like to thank Professor Bob Hardt for leading our PFUG, and we thank the undergraduate members Siegfried Bilstein, Kirby Fears, Michael Jauch, James Katz, and Caroline Nganga.
[B01] S. Berger, Edge Length Minimizing Polyhedra , Thesis, Rice University, (2001)
[M65] Z.A. Melzack, Problems connected with convexity , Canad. Math. Bull. 8 , (1965), 565-573.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?