| << Chapter < Page | Chapter >> Page > |
Question: How can Avogadro’s number be expressed in scientific notation?
Solution: Avogadro’s number can be written as the product of a real number (6.023) by the term (100,000,000,000,000,000,000,000)
Rather than trying to perform calculations using the decimal form for Avogadro’s number, chemists have learned to appreciate the more mathematically tractable scientific notation form of this important constant.
Engineering notation is quite similar to scientific notation. Numbers are written in engineering notation in the following form
where the coefficient a is a real number in the range 1<| a |<1,000 and the exponent c is restricted to be an integer multiple of 3.
An additional restriction on the coefficient ( a ) requires that a be expressed using no more than 3 significant digits. The restriction that the exponent be an integer multiple of 3 allows the numbers that result from the transformation to engineering notation to be expressed using the standard prefixes associated with the Scientifique Internationale (SI) system of units.
Example (Width of the Asteroid Belt)
Let’s consider the following application of engineering notation. The width of the asteroid belt has been determined to be 280,000,000 m .
Question: What is the width of the asteroid belt expressed in engineering notation?
Solution: Let us begin by expressing this quantity using scientific notation
We notice that the exponent is not an integer multiple of 3, so this quantity is not yet expressed in engineering notation. We do know that
This quantity can be substituted into the previous equation to yield the expression for the width of the asteroid belt in engineering notation
We will begin our investigation of applications of exponents with a discussion of electrical power. Consider the electrical circuit diagram that shows a source voltage ( V ) attached to a resistor ( R ) to produce a current ( I ).
The relationship between V, R and I is summarized by Ohm’s Law
where V is measured in volts (V) , I is measured in amps (A), and R is measured in ohms (Ω).
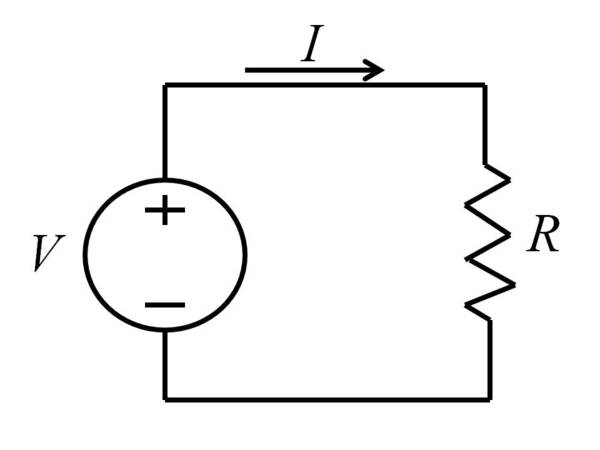
We may write an expression for the current as
The power that is absorbed by the resistor is known to be the product of the current flowing through the resistor time the potential difference (voltage) across the terminals of the resistor. If we denote the power absorbed by the resistor as P R , then it can be expressed mathematically as
Substitution of the expression for I obtained from Ohm’s Law yields an equivalent expression for the power absorbed by the resistor
Paying attention to the exponent, we can say that the power absorbed by the resistor is the square of the voltage across the terminals of the resistor divided by the resistance. The units associated with power are Watts (W).

Notification Switch
Would you like to follow the 'Math 1508 (laboratory) engineering applications of precalculus' conversation and receive update notifications?