| << Chapter < Page | Chapter >> Page > |
[Proof of the Lemma] Let be given, and assume without loss of generality that we know the letter of . We partition into -groups (that is, groups of letters) and into -groups. Because and are relatively prime, the initial letter of a -group will only coincide with the initial letter of a -group at the first letter of . Similarly, the final letter of a -group will only coincide with the final letter of a -group at the last letter of .
Since we know , it follows immediately that , and in general, if we know the letter of , we also know the letter of , and vice versa.
Take such that . Because is of the form of groups of repeated letters, and because we know , we also know the letters through , allowing us to fill in through . We repeat this process now on ; take such that and such that . This gives us through , which in turn gives us the corresponding letters for . Because of the condition described above about the initial and final letters of - and -groups, we will always be able to extend the range of uniquely determined letters at each step. We repeat this process until all of and are determined. Because and are finite, this process will terminate at a finite step.
Now, we can apply this Lemma to the claim above. In the case where , there is some for which or . In either case, this uniquely determines the corresponding and : They must be both 0 in the former case and both 1 in the latter case. Applying Lemma 4.2, we get a unique pair with .
In the case where , there are no 0s or 2s, so we must make a choice. We can choose either and , or and , but nothing else. With either choice, by Lemma 4.2, the rest of and are uniquely determined. These two choices correspond to the two pairs given above.
Thus, for all but one , there is a unique pair for which . Since there are unique pairs of and , there must be exactly elements , as desired.
This Proposition leads us to several results regarding the set , presented here as Corollaries.
Corollary 4.3 The set of offsets of contains exactly elements for all but finitely many .
This is an easy consequence of the Proposition and the construction of above.
Corollary 4.4 The set has zero Lebesgue measure for all .
This is an improvement of the result of Lemma 3.2. It is clear that a set in this form (defined by a set of offsets and a scaling factor ) has length at the stage bounded by
so that its Lebesgue measure must be bounded by
implying that when . In this case, we have and , so that when , as desired. To see this result graphically, see [link] .

The next result from this study involves the results from Theorems 3.4 and 3.5. Using the notation developed above, we can compute algorithmically the value for any rational . Recall that this value is already known for irrational . To do this, we need the following proposition.
Proposition 4.5 The set if and only if there are no gaps in the first stage of its construction.
[Proof of the Proposition] : Remember that is the union of intervals of length with left endpoints at the offsets in the set . We have
so that
In particular,
as desired.
: Assume that . Thus, must contain a gap of positive length, and this gap must show up in a finite stage, so it must be a scaled-down copy (or the overlap of multiple scaled-down copies) of a gap/gaps in the first stage of the construction . Thus, , as desired.
This Proposition tells us that is the unique point for which
This point can be computed by finding all the offsets of , ordering them from least to greatest, and checking the differences of adjacent offsets against . This has been done for several values of in [link] .
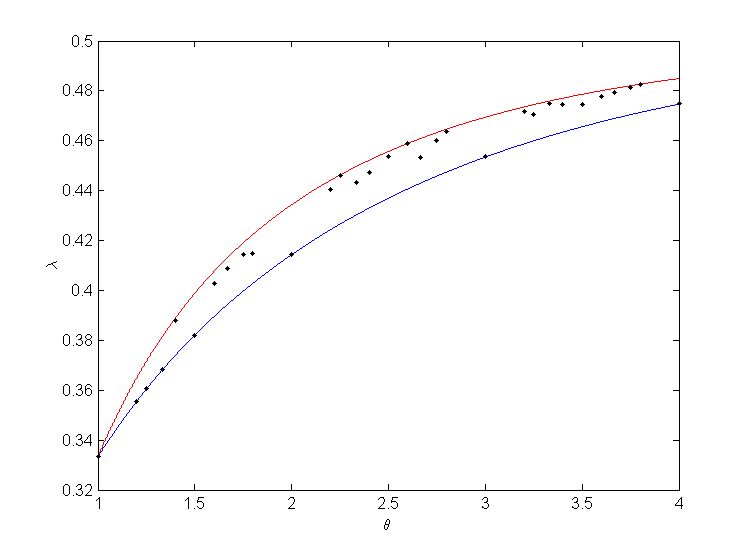
The question of what happens below these points and above the points given by Corollary 4.4 is still open. We conjecture that strictly between these points, is an M -Cantorval, and that at the points given by Corollary 4.4, where is a Cantor set with Hausdorff dimension 1 and zero Lebesgue measure.
This Connexions module describes work conducted as part of Rice University's VIGRE program, supported by National Science Foundation grant DMS–0739420.
We would also like to thank Dr. Danijela Damjanović and Dr. David Damanik for leading this study.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?