1. Home
  2. Chemistry
  3. Electronic structure and periodic
  4. The bohr model

6.2 The bohr model  (Page 4/9)

<< Chapter < Page
  Chemistry     Page 4 / 9
Chapter >> Page >
The figure includes a diagram representing the relative energy levels of the quantum numbers of the hydrogen atom. An upward pointing arrow at the left of the diagram is labeled, “E.” A grey shaded vertically oriented rectangle is placed just right of the arrow. The rectangle height matches the arrow length. Colored, horizontal line segments are placed inside the rectangle and labels are placed to the right of the box, arranged in a column with the heading, “Energy, n.” At the very base of the rectangle, a purple horizontal line segment is drawn. A black line extends to the right to the label, “1.” At a level approximately three-quarters of the distance to the top of the rectangle, a blue horizontal line segment is drawn. A black line extends to the right to the label, “2.” At a level approximately seven-eighths the distance from the base of the rectangle, a green horizontal line segment is drawn. A black line extends to the right to the label, “3.” Just a short distance above this segment, an orange horizontal line segment is drawn. A black line segment extends to the right to the label, “4.” Just above this segment, a red horizontal line segment is drawn. A black line extends to the right to the label, “5.” Just a short distance above this segment, a brown horizontal line segment is drawn. A black line extends to the right to the label, “infinity.” Arrows are drawn to depict energies of photons absorbed, as shown by upward pointing arrows on the left, or released as shown by downward pointing arrows on the right side of the diagram between the colored line segments. The label, “Electron moves to higher energy as light is absorbed,” is placed beneath the upward pointing arrows. Similarly, the label, “Electron moves to lower energy as light is emitted,” appears beneath the downward pointing arrows. Moving left to right across the diagram, arrows extend from one colored line segment to the next in the following order: purple to blue, purple to green, purple to orange, purple to red, purple to brown, blue to green, blue to orange, and blue to red. The arrows originating from the same colored segment are grouped together by close placement of the arrows. Similarly, the downward arrows follow in this sequence; brown to purple, red to purple, orange to purple, green to purple, blue to purple, red to blue, orange to blue, and green to blue. Arrows are again grouped by close placement according to the color at which the arrows end.
The horizontal lines show the relative energy of orbits in the Bohr model of the hydrogen atom, and the vertical arrows depict the energy of photons absorbed (left) or emitted (right) as electrons move between these orbits.

Calculating the energy and wavelength of electron transitions in a one–electron (bohr) system

What is the energy (in joules) and the wavelength (in meters) of the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 4 to the orbit with n = 6? In what part of the electromagnetic spectrum do we find this radiation?

Solution

In this case, the electron starts out with n = 4, so n 1 = 4. It comes to rest in the n = 6 orbit, so n 2 = 6. The difference in energy between the two states is given by this expression:

Δ E = E 1 − E 2 = 2.179 × 10 −18 ( 1 n 1 2 − 1 n 2 2 )
Δ E = 2.179 × 10 −18 ( 1 4 2 − 1 6 2 ) J
Δ E = 2.179 × 10 −18 ( 1 16 − 1 36 ) J
Δ E = 7.566 × 10 −20 J

This energy difference is positive, indicating a photon enters the system (is absorbed) to excite the electron from the n = 4 orbit up to the n = 6 orbit. The wavelength of a photon with this energy is found by the expression E = h c λ . Rearrangement gives:

λ = h c E
= ( 6.626 × 10 −34 J s ) × 2.998 × 10 8 m s −1 7.566 × 10 −20 J = 2.626 × 10 −6 m

From [link] , we can see that this wavelength is found in the infrared portion of the electromagnetic spectrum.

Check your learning

What is the energy in joules and the wavelength in meters of the photon produced when an electron falls from the n = 5 to the n = 3 level in a He + ion ( Z = 2 for He + )?

Answer:

6.198 × 10 –19 J; 3.205 × 10 −7 m

Got questions? Get instant answers now!

Bohr’s model of the hydrogen atom provides insight into the behavior of matter at the microscopic level, but it is does not account for electron–electron interactions in atoms with more than one electron. It does introduce several important features of all models used to describe the distribution of electrons in an atom. These features include the following:

  • The energies of electrons (energy levels) in an atom are quantized, described by quantum numbers : integer numbers having only specific allowed value and used to characterize the arrangement of electrons in an atom.
  • An electron’s energy increases with increasing distance from the nucleus.
  • The discrete energies (lines) in the spectra of the elements result from quantized electronic energies.

Of these features, the most important is the postulate of quantized energy levels for an electron in an atom. As a consequence, the model laid the foundation for the quantum mechanical model of the atom. Bohr won a Nobel Prize in Physics for his contributions to our understanding of the structure of atoms and how that is related to line spectra emissions.

Key concepts and summary

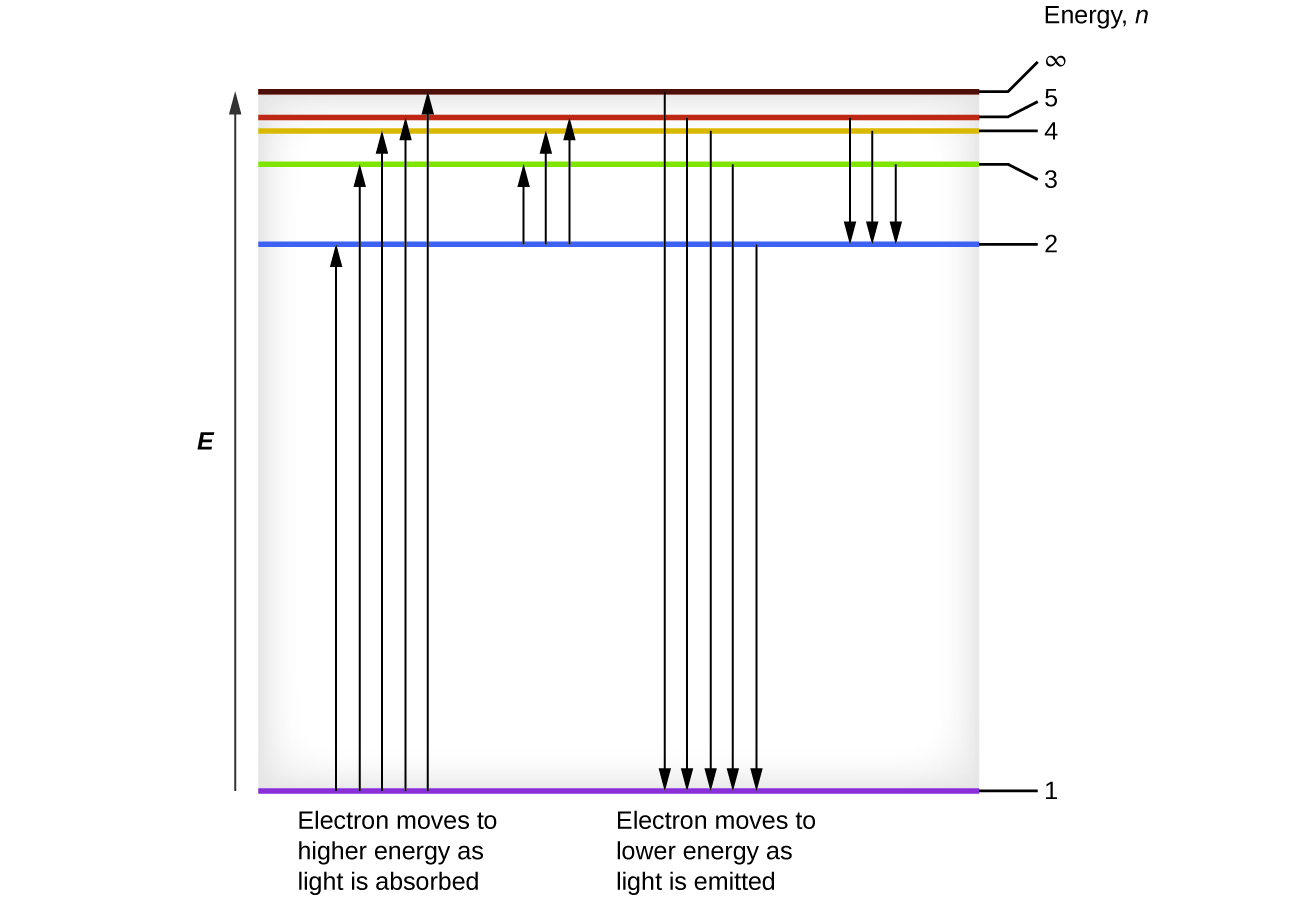
Bohr incorporated Planck’s and Einstein’s quantization ideas into a model of the hydrogen atom that resolved the paradox of atom stability and discrete spectra. The Bohr model of the hydrogen atom explains the connection between the quantization of photons and the quantized emission from atoms. Bohr described the hydrogen atom in terms of an electron moving in a circular orbit about a nucleus. He postulated that the electron was restricted to certain orbits characterized by discrete energies. Transitions between these allowed orbits result in the absorption or emission of photons. When an electron moves from a higher-energy orbit to a more stable one, energy is emitted in the form of a photon. To move an electron from a stable orbit to a more excited one, a photon of energy must be absorbed. Using the Bohr model, we can calculate the energy of an electron and the radius of its orbit in any one-electron system.

Questions & Answers

what's Thermochemistry
rhoda Reply
the study of the heat energy which is associated with chemical reactions
Kaddija
How was CH4 and o2 was able to produce (Co2)and (H2o
Edafe Reply
explain please
Victory
First twenty elements with their valences
Martine Reply
what is chemistry
asue Reply
what is atom
asue
what is the best way to define periodic table for jamb
Damilola Reply
what is the change of matter from one state to another
Elijah Reply
what is isolation of organic compounds
IKyernum Reply
what is atomic radius
ThankGod Reply
Read Chapter 6, section 5
Dr
Read Chapter 6, section 5
Kareem
Atomic radius is the radius of the atom and is also called the orbital radius
Kareem
atomic radius is the distance between the nucleus of an atom and its valence shell
Amos
Read Chapter 6, section 5
paulino
Bohr's model of the theory atom
Ayom Reply
is there a question?
Dr
when a gas is compressed why it becomes hot?
ATOMIC
It has no oxygen then
Goldyei
read the chapter on thermochemistry...the sections on "PV" work and the First Law of Thermodynamics should help..
Dr
Which element react with water
Mukthar Reply
Mgo
Ibeh
an increase in the pressure of a gas results in the decrease of its
Valentina Reply
definition of the periodic table
Cosmos Reply
What is the lkenes
Da Reply
what were atoms composed of?
Moses Reply
what is chemistry
Imoh Reply
what is chemistry
Damilola
<< Chapter < Page Page > Chapter >>
Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Chemistry. OpenStax CNX. May 20, 2015 Download for free at http://legacy.cnx.org/content/col11760/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Chemistry' conversation and receive update notifications?

Ask