| << Chapter < Page | Chapter >> Page > |
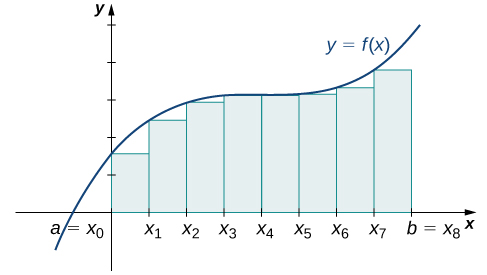
[link] shows the same curve divided into eight subintervals. Comparing the graph with four rectangles in [link] with this graph with eight rectangles, we can see there appears to be less white space under the curve when This white space is area under the curve we are unable to include using our approximation. The area of the rectangles is
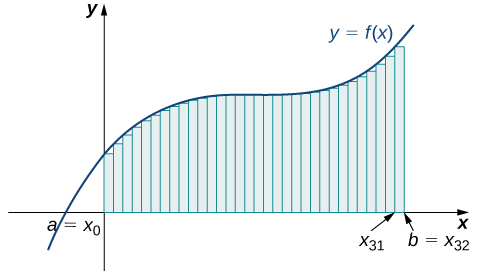
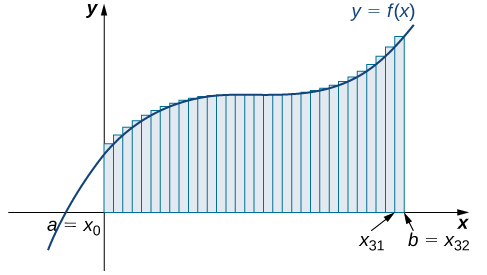
The graph in [link] shows the same function with 32 rectangles inscribed under the curve. There appears to be little white space left. The area occupied by the rectangles is
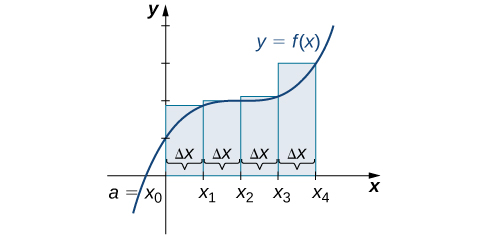
We can carry out a similar process for the right-endpoint approximation method. A right-endpoint approximation of the same curve, using four rectangles ( [link] ), yields an area
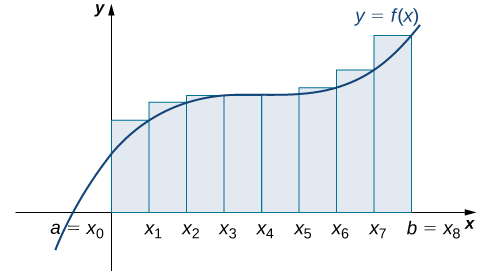
Dividing the region over the interval into eight rectangles results in The graph is shown in [link] . The area is
Last, the right-endpoint approximation with is close to the actual area ( [link] ). The area is approximately
Based on these figures and calculations, it appears we are on the right track; the rectangles appear to approximate the area under the curve better as n gets larger. Furthermore, as n increases, both the left-endpoint and right-endpoint approximations appear to approach an area of 8 square units. [link] shows a numerical comparison of the left- and right-endpoint methods. The idea that the approximations of the area under the curve get better and better as n gets larger and larger is very important, and we now explore this idea in more detail.
| Values of n | Approximate Area L n | Approximate Area R n |
|---|---|---|
| 7.5 | 8.5 | |
| 7.75 | 8.25 | |
| 7.94 | 8.06 |
So far we have been using rectangles to approximate the area under a curve. The heights of these rectangles have been determined by evaluating the function at either the right or left endpoints of the subinterval In reality, there is no reason to restrict evaluation of the function to one of these two points only. We could evaluate the function at any point c i in the subinterval and use as the height of our rectangle. This gives us an estimate for the area of the form

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?