2.4 Continuity (Page 3/16)

<< Chapter < Page

Calculus volume 1 Page 3 / 16

Chapter >> Page >

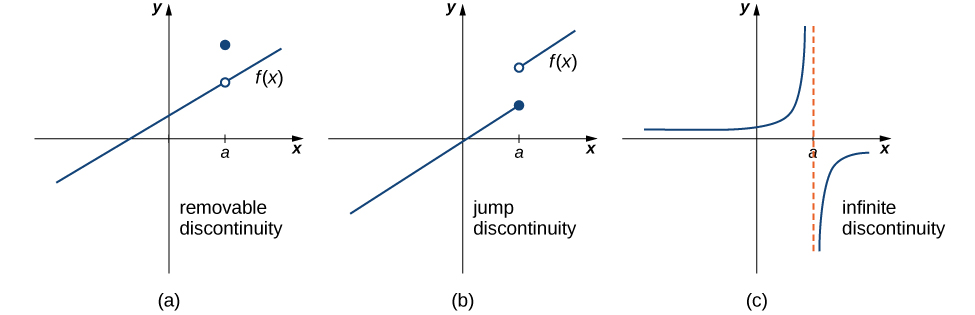
Three graphs, each showing a different discontinuity. The first is removable discontinuity. Here, the given function is a line with positive slope. At a point x=a, where a>0, there is an open circle on the line and a closed circle a few units above the line. The second is a jump discontinuity. Here, there are two lines with positive slope. The first line exists for x<=a, and the second exists for x>a, where a>0. The first line ends at a solid circle where x=a, and the second begins a few units up with an open circle at x=a. The third discontinuity type is infinite discontinuity. Here, the function has two parts separated by an asymptote x=a. The first segment is a curve stretching along the x axis to 0 as x goes to negative infinity and along the y axis to infinity as x goes to zero. The second segment is a curve stretching along the y axis to negative infinity as x goes to zero and along the x axis to 0 as x goes to infinity. — Discontinuities are classified as (a) removable, (b) jump, or (c) infinite.

These three discontinuities are formally defined as follows:

Definition

If $f (x)$ is discontinuous at a , then

$f$ has a removable discontinuity at a if $lim_{x \to a} f (x)$ exists. (Note: When we state that $lim_{x \to a} f (x)$ exists, we mean that $lim_{x \to a} f (x) = L,$ where L is a real number.)
$f$ has a jump discontinuity at a if $lim_{x \to a^{-}} f (x)$ and $lim_{x \to a^{+}} f (x)$ both exist, but $lim_{x \to a^{-}} f (x) \neq lim_{x \to a^{+}} f (x) .$ (Note: When we state that $lim_{x \to a^{-}} f (x)$ and $lim_{x \to a^{+}} f (x)$ both exist, we mean that both are real-valued and that neither take on the values ±∞.)
$f$ has an infinite discontinuity at a if $lim_{x \to a^{-}} f (x) = ± \infty$ or $lim_{x \to a^{+}} f (x) = ± \infty .$

Classifying a discontinuity

In [link] , we showed that $f (x) = \frac{x^{2} - 4}{x - 2}$ is discontinuous at $x = 2 .$ Classify this discontinuity as removable, jump, or infinite.

To classify the discontinuity at 2 we must evaluate $lim_{x \to 2} f (x) :$

\begin{matrix} lim_{x \to 2} f (x) & = lim_{x \to 2} \frac{x^{2} - 4}{x - 2} \\ = lim_{x \to 2} \frac{(x - 2) (x + 2)}{x - 2} \\ = lim_{x \to 2} (x + 2) \\ = 4 . \end{matrix}

Since f is discontinuous at 2 and $lim_{x \to 2} f (x)$ exists, f has a removable discontinuity at $x = 2 .$

Got questions? Get instant answers now!

Classifying a discontinuity

In [link] , we showed that $f (x) = {\begin{matrix} - x^{2} + 4 & if x \leq 3 \\ 4 x - 8 & if x > 3 \end{matrix}$ is discontinuous at $x = 3 .$ Classify this discontinuity as removable, jump, or infinite.

Earlier, we showed that f is discontinuous at 3 because $lim_{x \to 3} f (x)$ does not exist. However, since $lim_{x \to 3^{-}} f (x) = −5$ and $lim_{x \to 3^{-}} f (x) = 4$ both exist, we conclude that the function has a jump discontinuity at 3.

Got questions? Get instant answers now!

Classifying a discontinuity

Determine whether $f (x) = \frac{x + 2}{x + 1}$ is continuous at −1. If the function is discontinuous at −1, classify the discontinuity as removable, jump, or infinite.

The function value $f (−1)$ is undefined. Therefore, the function is not continuous at −1. To determine the type of discontinuity, we must determine the limit at −1. We see that $lim_{x \to {−1}^{-}} \frac{x + 2}{x + 1} = − \infty$ and $lim_{x \to {−1}^{+}} \frac{x + 2}{x + 1} = + \infty .$ Therefore, the function has an infinite discontinuity at −1.

Got questions? Get instant answers now!

For $f (x) = {\begin{matrix} x^{2} & if x \neq 1 \\ 3 & if x = 1 \end{matrix},$ decide whether f is continuous at 1. If f is not continuous at 1, classify the discontinuity as removable, jump, or infinite.

Discontinuous at 1; removable

Got questions? Get instant answers now!

Continuity over an interval

Now that we have explored the concept of continuity at a point, we extend that idea to continuity over an interval . As we develop this idea for different types of intervals, it may be useful to keep in mind the intuitive idea that a function is continuous over an interval if we can use a pencil to trace the function between any two points in the interval without lifting the pencil from the paper. In preparation for defining continuity on an interval, we begin by looking at the definition of what it means for a function to be continuous from the right at a point and continuous from the left at a point.

Continuity from the right and from the left

A function $f (x)$ is said to be continuous from the right at a if $lim_{x \to a^{+}} f (x) = f (a) .$

A function $f (x)$ is said to be continuous from the left at a if $lim_{x \to a^{-}} f (x) = f (a) .$

A function is continuous over an open interval if it is continuous at every point in the interval. A function $f (x)$ is continuous over a closed interval of the form $[a, b]$ if it is continuous at every point in $(a, b)$ and is continuous from the right at a and is continuous from the left at b . Analogously, a function $f (x)$ is continuous over an interval of the form $(a, b]$ if it is continuous over $(a, b)$ and is continuous from the left at b . Continuity over other types of intervals are defined in a similar fashion.

<< Chapter < Page Page > Chapter >>

Practice Key Terms 9

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?

Ask

©flickr: Urko	Music Reviewer MCQ By Edgar Delgado Start Quiz
	1 Business Law MCQ 1 By Maureen Miller Start Exam
	Are you a 5sos fan? By Rylee Minllic Start Quiz
	Classical Music By Marion Cabalfin Start Quiz
©flickr: Luis	Final Exam Review By Madison Christian Start Exam
	Biology By OpenStax Read Online Course
	25 AP 25 Urinary System MCQ By OpenStax Start Quiz
	Object Oriented Programming Test 1 By Ali Sid Start Test
©flickr:	Dairy Cattle Evaluation Exam By Katy Keilers Start Exam
	2 Endocrinology Essay By Rohini Ajay Start Test