| << Chapter < Page | Chapter >> Page > |
The first thing we need to do is define a frame of reference. We let represent the vertical distance below the top of the tank. That is, we orient the vertically, with the origin at the top of the tank and the downward direction being positive (see the following figure).
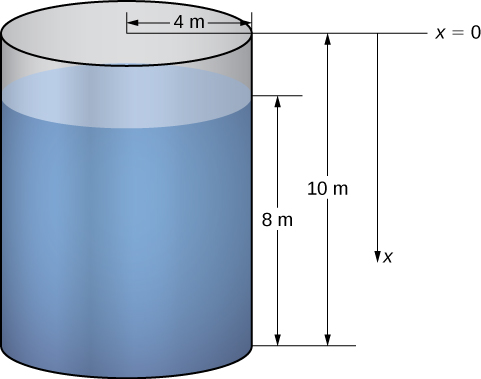
Using this coordinate system, the water extends from to Therefore, we partition the interval and look at the work required to lift each individual “layer” of water. So, for let be a regular partition of the interval and for choose an arbitrary point [link] shows a representative layer.
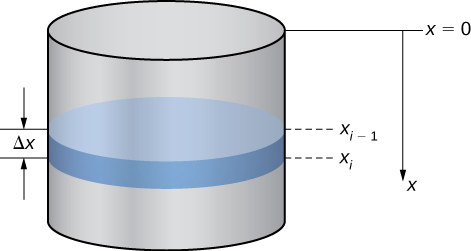
In pumping problems, the force required to lift the water to the top of the tank is the force required to overcome gravity, so it is equal to the weight of the water. Given that the weight-density of water is N/m 3 , or lb/ft 3 , calculating the volume of each layer gives us the weight. In this case, we have
Then, the force needed to lift each layer is
Note that this step becomes a little more difficult if we have a noncylindrical tank. We look at a noncylindrical tank in the next example.
We also need to know the distance the water must be lifted. Based on our choice of coordinate systems, we can use as an approximation of the distance the layer must be lifted. Then the work to lift the layer of water is approximately
Adding the work for each layer, we see the approximate work to empty the tank is given by
This is a Riemann sum, so taking the limit as we get
The work required to empty the tank is approximately 23,650,000 J.
For pumping problems, the calculations vary depending on the shape of the tank or container. The following problem-solving strategy lays out a step-by-step process for solving pumping problems.
We now apply this problem-solving strategy in an example with a noncylindrical tank.
Assume a tank in the shape of an inverted cone, with height ft and base radius ft. The tank is full to start with, and water is pumped over the upper edge of the tank until the height of the water remaining in the tank is ft. How much work is required to pump out that amount of water?
The tank is depicted in [link] . As we did in the example with the cylindrical tank, we orient the vertically, with the origin at the top of the tank and the downward direction being positive (step 1).
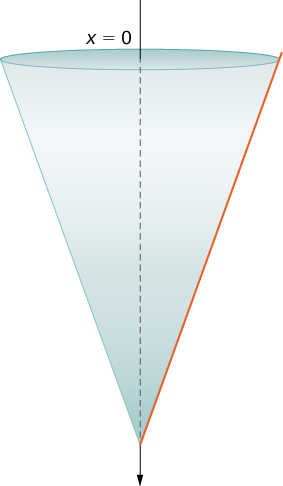
The tank starts out full and ends with ft of water left, so, based on our chosen frame of reference, we need to partition the interval Then, for let be a regular partition of the interval and for choose an arbitrary point We can approximate the volume of a layer by using a disk, then use similar triangles to find the radius of the disk (see the following figure).
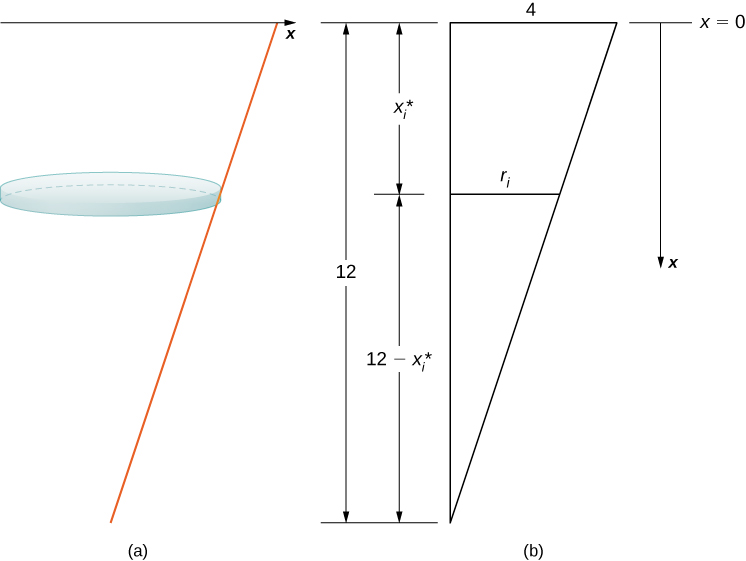
From properties of similar triangles, we have
Then the volume of the disk is
The weight-density of water is lb/ft 3 , so the force needed to lift each layer is approximately
Based on the diagram, the distance the water must be lifted is approximately feet (step 4), so the approximate work needed to lift the layer is
Summing the work required to lift all the layers, we get an approximate value of the total work:
Taking the limit as we obtain
It takes approximately ft-lb of work to empty the tank to the desired level.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?