| << Chapter < Page | Chapter >> Page > |
A tank is in the shape of an inverted cone, with height ft and base radius 6 ft. The tank is filled to a depth of 8 ft to start with, and water is pumped over the upper edge of the tank until 3 ft of water remain in the tank. How much work is required to pump out that amount of water?
Approximately ft-lb
In this last section, we look at the force and pressure exerted on an object submerged in a liquid. In the English system, force is measured in pounds. In the metric system, it is measured in newtons. Pressure is force per unit area, so in the English system we have pounds per square foot (or, perhaps more commonly, pounds per square inch, denoted psi). In the metric system we have newtons per square meter, also called pascals .
Let’s begin with the simple case of a plate of area submerged horizontally in water at a depth s ( [link] ). Then, the force exerted on the plate is simply the weight of the water above it, which is given by where is the weight density of water (weight per unit volume). To find the hydrostatic pressure —that is, the pressure exerted by water on a submerged object—we divide the force by the area. So the pressure is
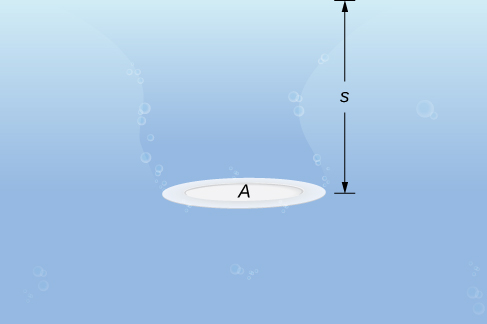
By Pascal’s principle , the pressure at a given depth is the same in all directions, so it does not matter if the plate is submerged horizontally or vertically. So, as long as we know the depth, we know the pressure. We can apply Pascal’s principle to find the force exerted on surfaces, such as dams, that are oriented vertically. We cannot apply the formula directly, because the depth varies from point to point on a vertically oriented surface. So, as we have done many times before, we form a partition, a Riemann sum, and, ultimately, a definite integral to calculate the force.
Suppose a thin plate is submerged in water. We choose our frame of reference such that the x -axis is oriented vertically, with the downward direction being positive, and point corresponding to a logical reference point. Let denote the depth at point x . Note we often let correspond to the surface of the water. In this case, depth at any point is simply given by However, in some cases we may want to select a different reference point for so we proceed with the development in the more general case. Last, let denote the width of the plate at the point
Assume the top edge of the plate is at point and the bottom edge of the plate is at point Then, for let be a regular partition of the interval and for choose an arbitrary point The partition divides the plate into several thin, rectangular strips (see the following figure).
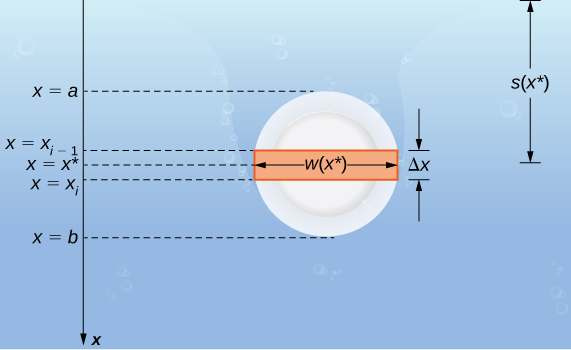
Let’s now estimate the force on a representative strip. If the strip is thin enough, we can treat it as if it is at a constant depth, We then have
Adding the forces, we get an estimate for the force on the plate:

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?