| << Chapter < Page | Chapter >> Page > |
Finding the y -intercept by substituting into the equation is easy, isn’t it? But we needed to use the Quadratic Formula to find the x -intercepts in [link] . We will use the Quadratic Formula again in the next example.
Graph .
 | |
| The equation
y has one side.
Since a is 2, the parabola opens upward. |
 |
| To find the axis of symmetry, find . |



The axis of symmetry is . |
| The vertex on the line |
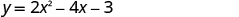 |
| Find y when . |
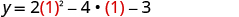


The vertex is . |
| The y -intercept occurs when |
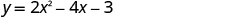 |
| Substitute |
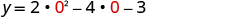 |
| Simplify. |

The y- intercept is . |
| The point
is one unit to the left of the line of symmetry.
The point one unit to the right of the line of symmetry is |
Point symmetric to the y- intercept is |
| The x -intercept occurs when . |
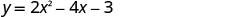 |
| Substitute . |
 |
| Use the Quadratic Formula. |
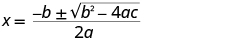 |
| Substitute in the values of a, b, c. |
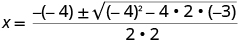 |
| Simplify. |
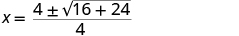 |
| Simplify inside the radical. |
 |
| Simplify the radical. |
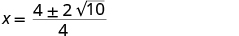 |
| Factor the GCF. |
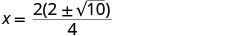 |
| Remove common factors. |
 |
| Write as two equations. |
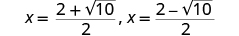 |
| Approximate the values. |
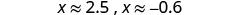 |
| The approximate values of the x- intercepts are and . | |
| Graph the parabola using the points found. |
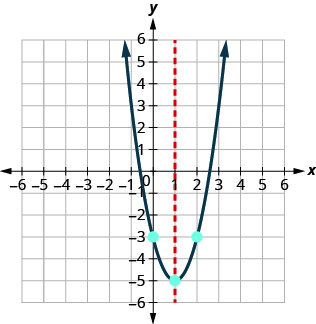 |
Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic equation. The y -coordinate of the vertex is the minimum y -value of a parabola that opens upward. It is the maximum y -value of a parabola that opens downward. See [link] .
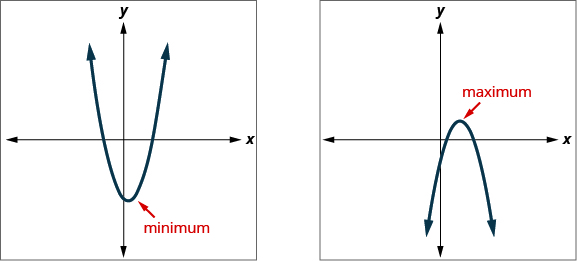
The y -coordinate of the vertex of the graph of a quadratic equation is the
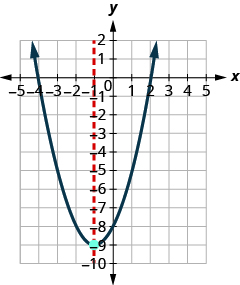
Find the minimum value of the quadratic equation .
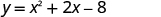 | |
| Since a is positive, the parabola opens upward. | |
| The quadratic equation has a minimum. | |
| Find the axis of symmetry. |

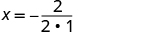

The axis of symmetry is . |
| The vertex is on the line |
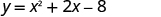 |
| Find y when |
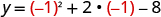
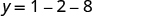

The vertex is . |
| Since the parabola has a minimum, the y- coordinate of the vertex is the minimum y- value of the quadratic equation. | |
| The minimum value of the quadratic is and it occurs when . | |
| Show the graph to verify the result. |
 |
Find the maximum or minimum value of the quadratic equation .
The minimum value is when .
Find the maximum or minimum value of the quadratic equation .
The maximum value is 5 when .
We have used the formula
to calculate the height in feet, , of an object shot upwards into the air with initial velocity, , after seconds.
This formula is a quadratic equation in the variable , so its graph is a parabola. By solving for the coordinates of the vertex, we can find how long it will take the object to reach its maximum height. Then, we can calculate the maximum height.
The quadratic equation models the height of a volleyball hit straight upwards with velocity 176 feet per second from a height of 4 feet.
Since a is negative, the parabola opens downward.
The quadratic equation has a maximum.
| Find h when . |

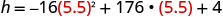 |
| Use a calculator to simplify. |
 |
| The vertex is . | |
| Since the parabola has a maximum, the h- coordinate of the vertex is the maximum y -value of the quadratic equation. | The maximum value of the quadratic is 488 feet and it occurs when seconds. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?