| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
We have learned how to solve inequalities in one variable. Now, we will look at inequalities in two variables. Inequalities in two variables have many applications. If you ran a business, for example, you would want your revenue to be greater than your costs—so that your business would make a profit.
A linear inequality is an inequality that can be written in one of the following forms:
where are not both zero.
Do you remember that an inequality with one variable had many solutions? The solution to the inequality is any number greater than 3. We showed this on the number line by shading in the number line to the right of 3, and putting an open parenthesis at 3. See [link] .

Similarly, inequalities in two variables have many solutions. Any ordered pair that makes the inequality true when we substitute in the values is a solution of the inequality.
An ordered pair is a solution of a linear inequality if the inequality is true when we substitute the values of x and y .
Determine whether each ordered pair is a solution to the inequality :
ⓐ ⓑ ⓒ ⓓ ⓔ
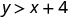 | |
 |
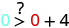 |
| Simplify. |
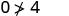
So, is not a solution to . |
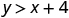 | |
 |
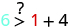 |
| Simplify. |
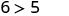
So, is a solution to . |
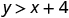 | |
 |
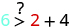 |
| Simplify. |

So, is not a solution to . |
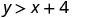 | |
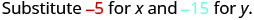 |
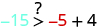 |
| Simplify. |
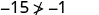
So, is not a solution to . |
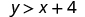 | |
 |
 |
| Simplify. |
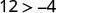
So, is a solution to . |
Determine whether each ordered pair is a solution to the inequality :
ⓐ ⓑ ⓒ ⓓ ⓔ
ⓐ yes ⓑ yes ⓒ yes ⓓ yes ⓔ no
Determine whether each ordered pair is a solution to the inequality :
ⓐ ⓑ ⓒ ⓓ ⓔ
ⓐ yes ⓑ yes ⓒ no ⓓ no ⓔ yes
Now, we will look at how the solutions of an inequality relate to its graph.
Let’s think about the number line in [link] again. The point separated that number line into two parts. On one side of 3 are all the numbers less than 3. On the other side of 3 all the numbers are greater than 3. See [link] .
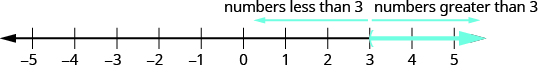
The solution to is the shaded part of the number line to the right of .
Similarly, the line separates the plane into two regions. On one side of the line are points with . On the other side of the line are the points with . We call the line a boundary line.
The line with equation is the boundary line that separates the region where from the region where .
For an inequality in one variable, the endpoint is shown with a parenthesis or a bracket depending on whether or not is included in the solution:

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?