| << Chapter < Page | Chapter >> Page > |

Similarly, for an inequality in two variables, the boundary line is shown with a solid or dashed line to indicate whether or not it the line is included in the solution. This is summarized in [link]
| Boundary line is not included in solution. | Boundary line is included in solution. |
| Boundary line is dashed. | Boundary line is solid. |
Now, let’s take a look at what we found in [link] . We’ll start by graphing the line , and then we’ll plot the five points we tested. See [link] .
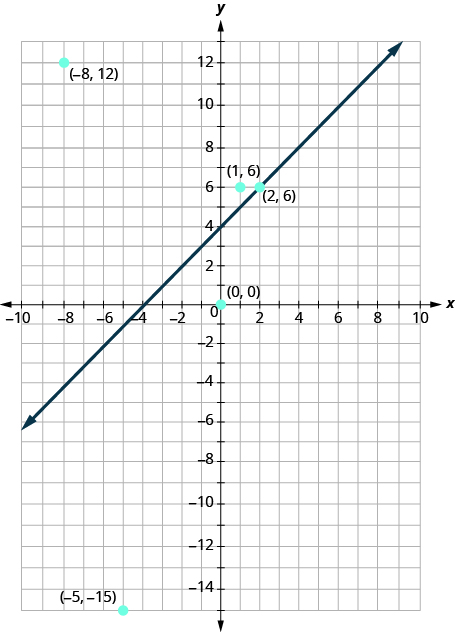
In [link] we found that some of the points were solutions to the inequality and some were not.
Which of the points we plotted are solutions to the inequality ? The points and are solutions to the inequality . Notice that they are both on the same side of the boundary line .
The two points and are on the other side of the boundary line , and they are not solutions to the inequality . For those two points, .
What about the point ? Because , the point is a solution to the equation . So the point is on the boundary line.
Let’s take another point on the left side of the boundary line and test whether or not it is a solution to the inequality . The point clearly looks to be to the left of the boundary line, doesn’t it? Is it a solution to the inequality?
Any point you choose on the left side of the boundary line is a solution to the inequality . All points on the left are solutions.
Similarly, all points on the right side of the boundary line, the side with and , are not solutions to . See [link] .
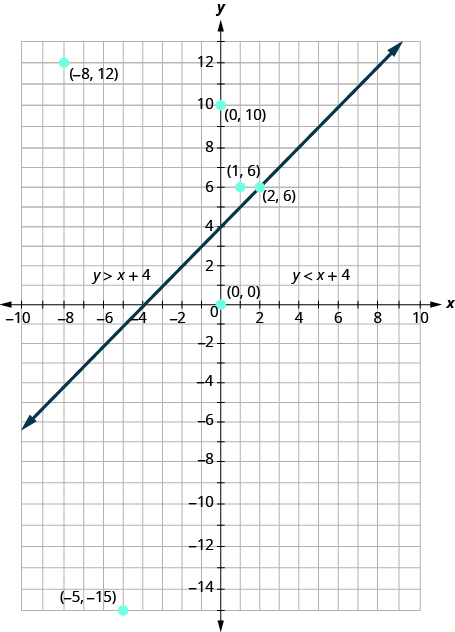
The graph of the inequality is shown in [link] below. The line divides the plane into two regions. The shaded side shows the solutions to the inequality .
The points on the boundary line, those where , are not solutions to the inequality , so the line itself is not part of the solution. We show that by making the line dashed, not solid.
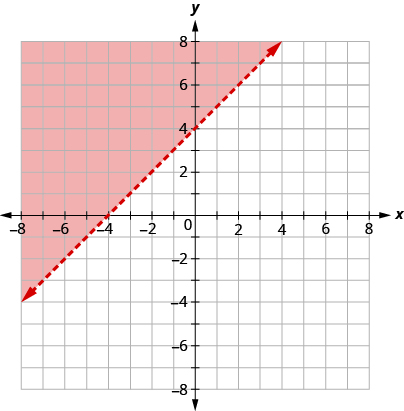
The boundary line shown is . Write the inequality shown by the graph.
The line is the boundary line. On one side of the line are the points with and on the other side of the line are the points with .
Let’s test the point and see which inequality describes its side of the boundary line.
At , which inequality is true:
Since, is true, the side of the line with , is the solution. The shaded region shows the solution of the inequality .
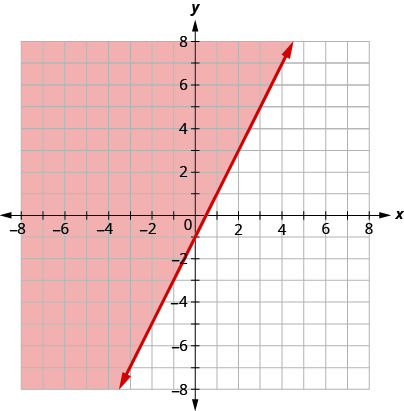
Since the boundary line is graphed with a solid line, the inequality includes the equal sign.
The graph shows the inequality .
We could use any point as a test point, provided it is not on the line. Why did we choose ? Because it’s the easiest to evaluate. You may want to pick a point on the other side of the boundary line and check that .
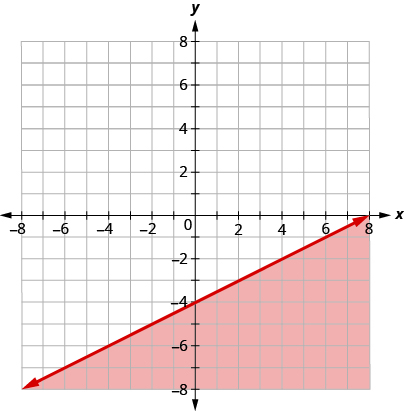
Write the inequality shown by the graph with the boundary line .
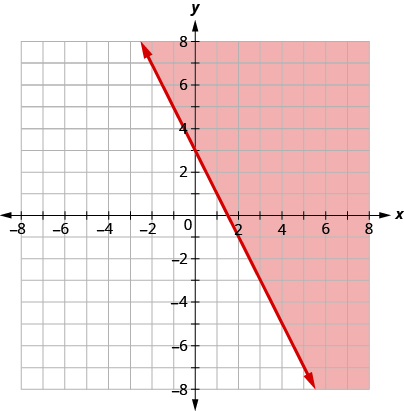
Write the inequality shown by the graph with the boundary line .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?