| << Chapter < Page | Chapter >> Page > |
Graph the equation .
We’ll let be 0, 1, and to find 3 points. The ordered pairs are shown in [link] . Plot the points, check that they line up, and draw the line. See [link] .
| 0 | ||
| 1 | ||
| 2 |
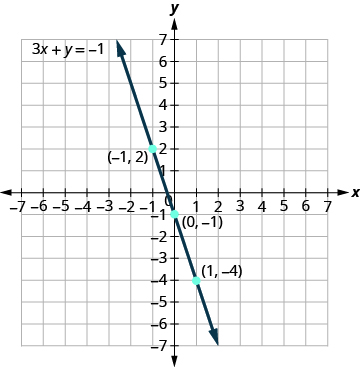
If you can choose any three points to graph a line, how will you know if your graph matches the one shown in the answers in the book? If the points where the graphs cross the x - and y -axis are the same, the graphs match!
The equation in [link] was written in standard form, with both and on the same side. We solved that equation for in just one step. But for other equations in standard form it is not that easy to solve for , so we will leave them in standard form. We can still find a first point to plot by letting and solving for . We can plot a second point by letting and then solving for . Then we will plot a third point by using some other value for or .
Graph the equation .
We list the ordered pairs in [link] . Plot the points, check that they line up, and draw the line. See [link] .
| 0 | ||
| 3 | 0 | |
| 6 | 2 |
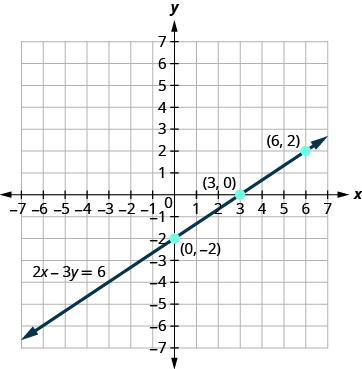
Can we graph an equation with only one variable? Just and no , or just without an ? How will we make a table of values to get the points to plot?
Let’s consider the equation . This equation has only one variable, . The equation says that is always equal to , so its value does not depend on . No matter what is, the value of is always .
So to make a table of values, write in for all the values. Then choose any values for . Since does not depend on , you can choose any numbers you like. But to fit the points on our coordinate graph, we’ll use 1, 2, and 3 for the y -coordinates. See [link] .
| 1 | ||
| 2 | ||
| 3 |
Plot the points from [link] and connect them with a straight line. Notice in [link] that we have graphed a vertical line .
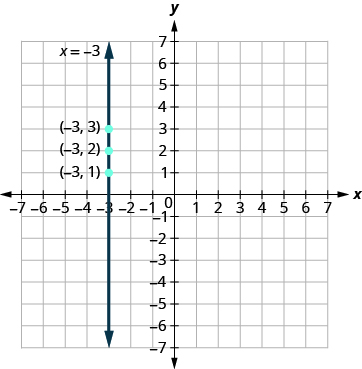
A vertical line is the graph of an equation of the form .
The line passes through the x -axis at .
Graph the equation .
The equation has only one variable, , and is always equal to 2. We create [link] where is always 2 and then put in any values for . The graph is a vertical line passing through the x -axis at 2. See [link] .
| 2 | 1 | |
| 2 | 2 | |
| 2 | 3 |

What if the equation has but no ? Let’s graph the equation . This time the y - value is a constant, so in this equation, does not depend on . Fill in 4 for all the ’s in [link] and then choose any values for . We’ll use 0, 2, and 4 for the x -coordinates.
| 0 | 4 | |
| 2 | 4 | |
| 4 | 4 |
The graph is a horizontal line passing through the y -axis at 4. See [link] .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?