| << Chapter < Page | Chapter >> Page > |
Sequences occur naturally in the growth patterns of nautilus shells, pinecones, tree branches, and many other natural structures. We may see the sequence in the leaf or branch arrangement, the number of petals of a flower, or the pattern of the chambers in a nautilus shell. Their growth follows the Fibonacci sequence, a famous sequence in which each term can be found by adding the preceding two terms. The numbers in the sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34,…. Other examples from the natural world that exhibit the Fibonacci sequence are the Calla Lily, which has just one petal, the Black-Eyed Susan with 13 petals, and different varieties of daisies that may have 21 or 34 petals.
Each term of the Fibonacci sequence depends on the terms that come before it. The Fibonacci sequence cannot easily be written using an explicit formula. Instead, we describe the sequence using a recursive formula , a formula that defines the terms of a sequence using previous terms.
A recursive formula always has two parts: the value of an initial term (or terms), and an equation defining in terms of preceding terms. For example, suppose we know the following:
We can find the subsequent terms of the sequence using the first term.
So the first four terms of the sequence are .
The recursive formula for the Fibonacci sequence states the first two terms and defines each successive term as the sum of the preceding two terms.
To find the tenth term of the sequence, for example, we would need to add the eighth and ninth terms. We were told previously that the eighth and ninth terms are 21 and 34, so
A recursive formula is a formula that defines each term of a sequence using preceding term(s). Recursive formulas must always state the initial term, or terms, of the sequence.
Must the first two terms always be given in a recursive formula?
No. The Fibonacci sequence defines each term using the two preceding terms, but many recursive formulas define each term using only one preceding term. These sequences need only the first term to be defined.
Given a recursive formula with only the first term provided, write the first terms of a sequence.
Write the first five terms of the sequence defined by the recursive formula.
The first term is given in the formula. For each subsequent term, we replace with the value of the preceding term.
The first five terms are See [link] .
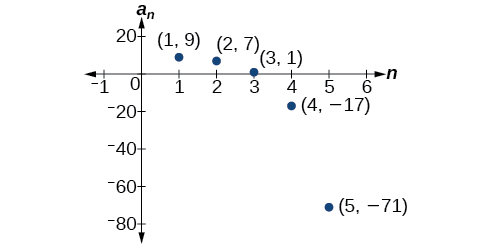

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?