| << Chapter < Page | Chapter >> Page > |
The coffee shop menu, shown in [link] consists of items and their prices.

Each item on the menu has only one price, so the price is a function of the item.
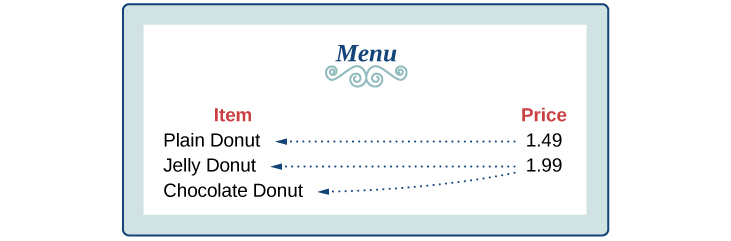
Therefore, the item is a not a function of price.
In a particular math class, the overall percent grade corresponds to a grade-point average. Is grade-point average a function of the percent grade? Is the percent grade a function of the grade-point average? [link] shows a possible rule for assigning grade points.
| Percent grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Grade-point average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
For any percent grade earned, there is an associated grade-point average, so the grade-point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.
In the grading system given, there is a range of percent grades that correspond to the same grade-point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade-point average.
[link] http://www.baseball-almanac.com/legendary/lisn100.shtml. Accessed 3/24/2014. lists the five greatest baseball players of all time in order of rank.
| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
a. yes; b. yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into graphing calculators and computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables for height and for age. The letters and are often used to represent functions just as we use and to represent numbers and and to represent sets.
Remember, we can use any letter to name the function; the notation shows us that depends on The value must be put into the function to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?