| << Chapter < Page | Chapter >> Page > |

Until the 1920s, the so-called spiral nebulae were believed to be clouds of dust and gas in our own galaxy, some tens of thousands of light years away. Then, astronomer Edwin Hubble proved that these objects are galaxies in their own right, at distances of millions of light years. Today, astronomers can detect galaxies that are billions of light years away. Distances in the universe can be measured in all directions. As such, it is useful to consider distance as an absolute value function. In this section, we will continue our investigation of absolute value functions .
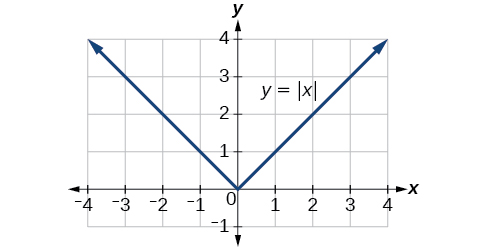
Recall that in its basic form the absolute value function is one of our toolkit functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign. Knowing this, we can use absolute value functions to solve some kinds of real-world problems.
The absolute value function can be defined as a piecewise function
Electrical parts, such as resistors and capacitors, come with specified values of their operating parameters: resistance, capacitance, etc. However, due to imprecision in manufacturing, the actual values of these parameters vary somewhat from piece to piece, even when they are supposed to be the same. The best that manufacturers can do is to try to guarantee that the variations will stay within a specified range, often or
Suppose we have a resistor rated at 680 ohms, Use the absolute value function to express the range of possible values of the actual resistance.
We can find that 5% of 680 ohms is 34 ohms. The absolute value of the difference between the actual and nominal resistance should not exceed the stated variability, so, with the resistance in ohms,
Students who score within 20 points of 80 will pass a test. Write this as a distance from 80 using absolute value notation.
using the variable for passing,
The most significant feature of the absolute value graph is the corner point at which the graph changes direction. This point is shown at the origin in [link] .
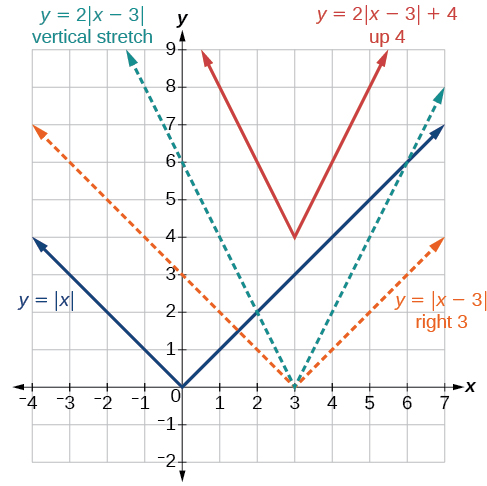
[link] shows the graph of The graph of has been shifted right 3 units, vertically stretched by a factor of 2, and shifted up 4 units. This means that the corner point is located at for this transformed function.
Write an equation for the function graphed in [link] .
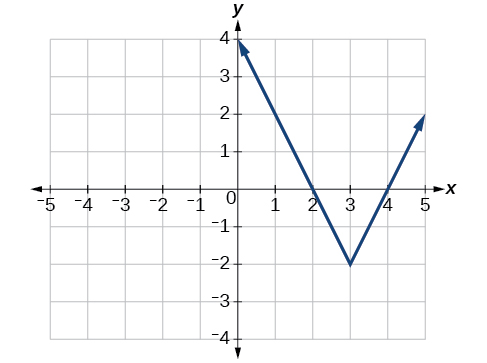
The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 units and down 2 units from the basic toolkit function. See [link] .
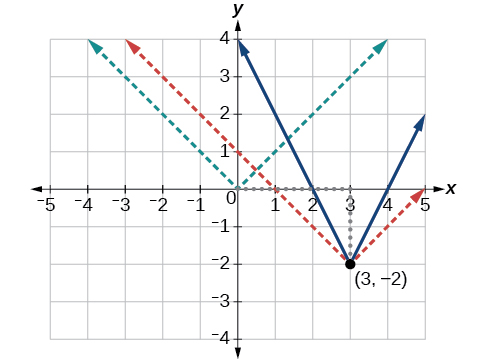
We also notice that the graph appears vertically stretched, because the width of the final graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as it would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance as shown in [link] .
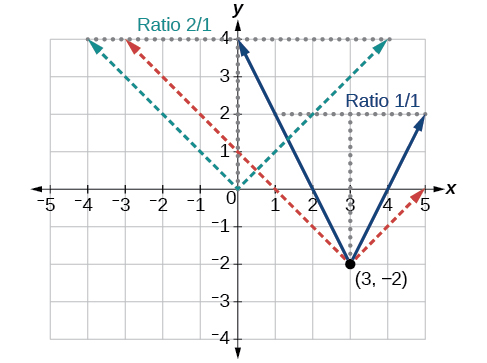
From this information we can write the equation

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?